题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)求证:“如果直线![]() 过点
过点![]() ,那么
,那么![]() ”是真命题;
”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)设出A,B两点的坐标根据向量的点乘运算求证即可,
(2)把(1)中题设和结论变换位置然后设出A,B两点的坐标根据向量运算求证即可.
试题解析:
证明:(1)设过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,
, ![]()
当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,此时,
,此时,
直线![]() 与抛物线相交于点
与抛物线相交于点![]() 、
、![]() ,∴
,∴![]()
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,其中
,其中![]()
由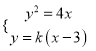 得
得![]() ,则
,则![]()
又∵![]() ,
, ![]() ,∴
,∴![]()
综上所述,命题“如果直线![]() 过点
过点![]() ,那么
,那么![]() ”是真命题.
”是真命题.
(2)逆命题是:设直线![]() 交抛物线
交抛物线![]() 于
于![]() 、
、![]() 两点,
两点,
如果![]() ,那么直线
,那么直线![]() 过点
过点![]() ,
,
该命题是假命题.
例如:取抛物线上的点![]() ,
, ![]() .此时
.此时![]()
直线![]() 的方程为
的方程为![]() ,而
,而![]() 不在直线
不在直线![]() 上.
上.

练习册系列答案
相关题目
【题目】某车间为了规定工时定额,需确定加工零件所花费的时间,为此做了4次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
若加工时间![]() 与零件个数
与零件个数![]() 之间有较好的相关关系.
之间有较好的相关关系.
(1)求加工时间与零件个数的线性回归方程![]() .
.
(2)试预报加工10个零件需要的时间.
附录:参考公式: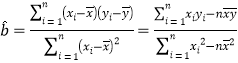 ,
,![]() .
.

