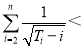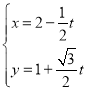题目内容
【题目】(本小题14分)在平面直角坐标系中,曲线C1的参数方程为![]() (a>b>0,
(a>b>0,![]() 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点![]() 对应的参数
对应的参数![]() .
.![]() 与曲线C2交于点
与曲线C2交于点![]() .
.
(1)求曲线C1,C2的直角坐标方程;
(2)![]() ,
,![]() 是曲线C1上的两点,求
是曲线C1上的两点,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】
试题(1)利用同角三角函数平方关系,消去参数![]() ,得曲线C1普通方程
,得曲线C1普通方程![]() ,先确定曲线C2极坐标方程ρ=2cosθ,再利用
,先确定曲线C2极坐标方程ρ=2cosθ,再利用![]() 将极坐标化为直角坐标方程:
将极坐标化为直角坐标方程:![]() (2)由题意得:
(2)由题意得:![]()
![]() ,∴
,∴![]() +
+![]() =(
=(![]() +
+![]() )+(
)+(![]() +
+![]() )=
)=![]() ..
..
试题解析:(1)将M(2,![]() )及对应的参数
)及对应的参数![]() =
=![]() ;θ=
;θ=![]() ;
;
代入![]() 得:
得: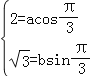 得:
得:![]()
∴曲线C1的方程为:![]() (
(![]() 为参数)即:
为参数)即:![]() .
.
设圆C2的半径R,则圆C2的方程为:ρ=2Rcosθ,将点D(![]() ,
,![]() )
)
代入得:![]() =2R
=2R![]() ∴R=1
∴R=1
∴圆C2的方程为:ρ=2cosθ即:![]() .
.
将A(ρ1,θ),Β(ρ2,θ+![]() )代入C1得:
)代入C1得:
![]()
![]()
∴![]() +
+![]() =(
=(![]() +
+![]() )+(
)+(![]() +
+![]() )=
)=![]() .
.

【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了止损,某地一水果店老板利用抖音直播卖货,经过一段时间对一种水果的销售情况进行统计,得到![]() 天的数据如下:
天的数据如下:
销售单价 |
|
|
|
|
|
销售量 |
|
|
|
|
|
(1)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)该水果店开展促销活动,当该水果销售单价为![]() 元/
元/![]() 时,其销售量达到
时,其销售量达到![]() ,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过
,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过![]() ,则认为所得到的回归直线方程是理想的,试问:(1)中得到的回归直线方程是否理想?
,则认为所得到的回归直线方程是理想的,试问:(1)中得到的回归直线方程是否理想?
(3)根据(1)的结果,若该水果成本是![]() 元/
元/![]() ,销售单价
,销售单价![]() 为何值时(销售单价不超过
为何值时(销售单价不超过![]() 元/
元/![]() ),该水果店利润的预计值最大?
),该水果店利润的预计值最大?
参考公式:回归直线方程![]() ,其中
,其中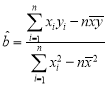 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
【题目】中国是茶的故乡,也是茶文化的发源地.中国茶的发现和利用已有四千七百多年的历史,且长盛不衰,传遍全球.为了弘扬中国茶文化,某酒店推出特色茶食品“金萱排骨茶”,为了解每壶“金萱排骨茶”中所放茶叶量![]() 克与食客的满意率
克与食客的满意率![]() 的关系,通过试验调查研究,发现可选择函数模型
的关系,通过试验调查研究,发现可选择函数模型![]() 来拟合
来拟合![]() 与
与![]() 的关系,根据以下数据:
的关系,根据以下数据:
茶叶量 | 1 | 2 | 3 | 4 | 5 |
| 4.34 | 4.36 | 4.44 | 4.45 | 4.51 |
可求得y关于x的回归方程为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
【题目】某化工厂在定期检修设备时发现生产管道中共有5处阀门(![]() )发生有害气体泄漏.每处阀门在每小时内有害气体的泄露量大体相等,约为0.01立方米.阀门的修复工作可在不停产的情况下实施.由于各阀门所处的位置不同,因此修复所需的时间不同,且修复时必须遵从一定的顺序关系,具体情况如下表:
)发生有害气体泄漏.每处阀门在每小时内有害气体的泄露量大体相等,约为0.01立方米.阀门的修复工作可在不停产的情况下实施.由于各阀门所处的位置不同,因此修复所需的时间不同,且修复时必须遵从一定的顺序关系,具体情况如下表:
泄露阀门 |
|
|
|
|
|
修复时间 (小时) | 11 | 8 | 5 | 9 | 6 |
需先修复 好的阀门 |
|
|
|
|
|
在只有一个阀门修复设备的情况下,合理安排修复顺序,泄露的有害气体总量最小为( )
A.1.14立方米B.1.07立方米C.1.04立方米D.0.39立方米