题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
如图所示
若存在Q,使PQ⊥QD ∵PA⊥QD, ∴DQ⊥AQ 则以AD为直径的圆与BC有交点,则 ∴a≥2 故当a≥2时,在BC上存在点Q,使PQ⊥QD |
(2) |
已知BC边上有且只有一点Q,使PQ⊥QD,则a=2,Q为BC中点.取AD的中点M,连结PM、QM,则QM⊥AD,PA⊥QM, ∴QM⊥平面PAD 设二面角Q-PD-A的大小为θ,cosθ= ∴二面角Q-PD-A的大小为arccos |

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目


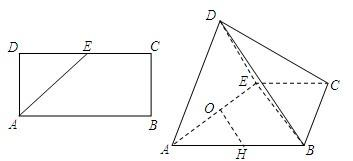 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2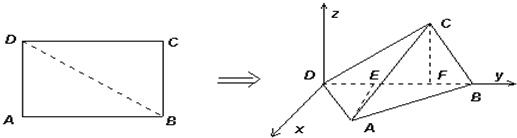
 (2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使
(2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使