题目内容
 (2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使DB=
(2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使DB=| 3 |
(Ⅰ)求证:平面AOD⊥平面ABCO;
(Ⅱ)求直线BC与平面ABD所成角的正弦值.
分析:(1)要证明面面垂直,常用其判定定理来证明,即在其中一个平面内找到一条直线与另一平面垂直;
(2)空间中求线面角,常用空间向量来解决,即建立空间直角坐标系后,求直线的方向向量与平面的法向量,再求其夹角的余弦即是所求.
(2)空间中求线面角,常用空间向量来解决,即建立空间直角坐标系后,求直线的方向向量与平面的法向量,再求其夹角的余弦即是所求.
解答:(Ⅰ)证明:∵在矩形ABCD中,AB=2AD=2,O为CD中点,
∴△AOD,△BOC为等腰直角三角形,
∴∠AOB=90°,即OB⊥OA.…(1分)
取AO中点H,连结DH,BH,则OH=DH=
,
在Rt△BOH中,BH2=BO2+OH2=
,
在△BHD中,DH2+BH2=(
)2+
=3,又DB2=3,
∴DH2+BH2=DB2,∴DH⊥BH.…(2分)
又DH⊥OA,OA∩BH=H …(3分)
∴DH⊥面ABCO,…(4分)
而DH∈平面AOD,…(5分)
∴平面AOD⊥平面ABCO.…(6分)
(Ⅱ)解:分别以直线OA,OB为x轴和y轴,O为坐标原点,建立如图所示的空间直角坐标系,
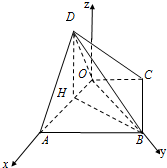
则B(0,
,0),A(
,0,0),D(
,0,
),C(-
,
,0).
∴
=(-
,
,0),
=(-
,0,
),
=(-
,-
,0).…(7分)
设平面ABD的一个法向量为n=(x,y,z),
由
得
即x=y,x=z,令x=1,则y=z-1,
取n=(1,1,1).…(9分)
设α为直线BC与平面ABD所成的角,
则sinα=
=
=
.…(11分)
即直线BC与平面ABD所成角的正弦值为
.…(12分)
∴△AOD,△BOC为等腰直角三角形,
∴∠AOB=90°,即OB⊥OA.…(1分)
取AO中点H,连结DH,BH,则OH=DH=
| ||
| 2 |
在Rt△BOH中,BH2=BO2+OH2=
| 5 |
| 2 |
在△BHD中,DH2+BH2=(
| ||
| 2 |
| 5 |
| 2 |
∴DH2+BH2=DB2,∴DH⊥BH.…(2分)
又DH⊥OA,OA∩BH=H …(3分)
∴DH⊥面ABCO,…(4分)
而DH∈平面AOD,…(5分)
∴平面AOD⊥平面ABCO.…(6分)
(Ⅱ)解:分别以直线OA,OB为x轴和y轴,O为坐标原点,建立如图所示的空间直角坐标系,

则B(0,
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| AB |
| 2 |
| 2 |
| AD |
| ||
| 2 |
| ||
| 2 |
| BC |
| ||
| 2 |
| ||
| 2 |
设平面ABD的一个法向量为n=(x,y,z),
由
|
|
即x=y,x=z,令x=1,则y=z-1,
取n=(1,1,1).…(9分)
设α为直线BC与平面ABD所成的角,
则sinα=
|
| ||
|
|
| ||
|
| ||
| 3 |
即直线BC与平面ABD所成角的正弦值为
| ||
| 3 |
点评:本题考查的内容是立体几何,主要考查面面垂直的证明以及求线面角中的向量方法,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目