题目内容
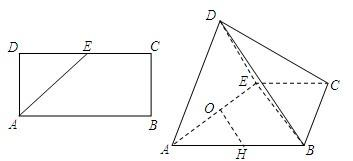 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将△AED折起,使DB=2| 3 |
(1)求证:直线OH∥面BDE;
(2)求证:面ADE⊥面ABCE.
分析:(1)要证:直线OH∥面BDE,只需证明OH∥EB即可;
(2)要证:面ADE⊥面ABCE,只需证明DO⊥AE,DO⊥OB 即 DO⊥面ABCE即可.
(2)要证:面ADE⊥面ABCE,只需证明DO⊥AE,DO⊥OB 即 DO⊥面ABCE即可.
解答:解:(1)证明:∵O、H分别为AE、AB的中点
∴OH∥BE,又OH不在面BDE内
∴直线OH∥面BDE.
(2)O为AE的中点AD=DE,
∴DO⊥AE,
∵DO=
,DB=2
,BO2=10
∴DB2=DO2+BO2
∴DO⊥OB又因为AE和BO是相交直线
所以,DO⊥面ABCE,又OD在面ADE内
∴面ADE⊥面ABCE.
∴OH∥BE,又OH不在面BDE内
∴直线OH∥面BDE.
(2)O为AE的中点AD=DE,
∴DO⊥AE,
∵DO=
| 2 |
| 3 |
∴DB2=DO2+BO2
∴DO⊥OB又因为AE和BO是相交直线
所以,DO⊥面ABCE,又OD在面ADE内
∴面ADE⊥面ABCE.
点评:本题考查直线与平面平行和垂直的判定,考查学生逻辑思维能力,是基础题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
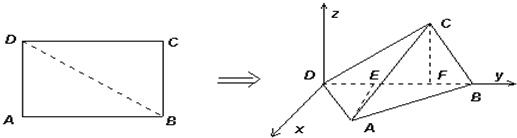
 (2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使
(2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使