题目内容
已知矩形ABCD中，AB=6，BC=6
，E为AD的中点（图一）．沿BE将△ABE折起，使平面ABE⊥平面BECD（图二），且F为AC的中点．
（1）求证：FD∥平面ABE；
（2）求证：AC⊥BE．
| 2 |
（1）求证：FD∥平面ABE；
（2）求证：AC⊥BE．
分析：（1）证明平面DFM∥平面ABE，可得FD∥平面ABE．在图2中，设M为BC的中点，连DM、MF，可证MF∥平面ABE，MD∥平面ABE；
（2）在矩形ABCD（图1）中，连AC，交BE于G，利用向量方法证明AC⊥BE，从而可知BE⊥平面AGC．
（2）在矩形ABCD（图1）中，连AC，交BE于G，利用向量方法证明AC⊥BE，从而可知BE⊥平面AGC．
解答：证明：（1）在图2中，设M为BC的中点，连DM、MF．
∵F为AC的中点，M为BC的中点
∴MF∥AB…（2分）
∵MF?平面ABE
∴MF∥平面ABE
又∵BM∥DE且BM=DE，∴四边形BMDE为平行四边形
∴MD∥BE
∵MD?平面ABE
∴MD∥平面ABE
∵MF∩MD=M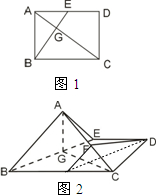
∴平面DFM∥平面ABE…（4分）
∵FD?平面DFM
∴FD∥平面ABE；…（6分）
（2）在矩形ABCD（图1）中，连AC，交BE于G．
∴
•
=(
+
)•(
+
)=-
2+
•
=-36+36=0
∴AC⊥BE…（8分）
∴在图二中，AG⊥BE，CG⊥BE，AG∩CG=G
∴BE⊥平面AGC …（10分），
又∵AC?平面AGC，∴AC⊥BE．…（12分）
∵F为AC的中点，M为BC的中点
∴MF∥AB…（2分）
∵MF?平面ABE
∴MF∥平面ABE
又∵BM∥DE且BM=DE，∴四边形BMDE为平行四边形
∴MD∥BE
∵MD?平面ABE
∴MD∥平面ABE
∵MF∩MD=M
∴平面DFM∥平面ABE…（4分）
∵FD?平面DFM
∴FD∥平面ABE；…（6分）
（2）在矩形ABCD（图1）中，连AC，交BE于G．
∴
| BE |
| AC |
| BA |
| AE |
| AB |
| BC |
| AB |
| AE |
| BC |
∴AC⊥BE…（8分）
∴在图二中，AG⊥BE，CG⊥BE，AG∩CG=G
∴BE⊥平面AGC …（10分），
又∵AC?平面AGC，∴AC⊥BE．…（12分）
点评：本题考查线面平行，考查线面垂直、线线垂直，解题的关键是掌握线面平行的判断方法．
练习册系列答案
相关题目
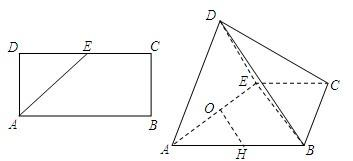已知矩形ABCD中，AB=2AD=4，E为CD的中点，沿AE将△AED折起，使DB=2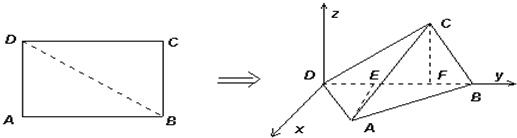
（2013•临沂二模）如图，已知矩形ABCD中，AB=2AD=2，O为CD的中点，沿AO将三角形AOD折起，使