题目内容
【题目】已知椭圆C：
+
=1（a＞b＞0）的离心率为
， 焦距为2
， 过点D（1，0）且不过点E（2，1）的直线l与椭圆C交于A，B两点，直线AE与直线x=3交于点M．
（1）求椭圆C的标准方程；
（2）若AB垂直于x轴，求直线MB的斜率。
【答案】解：（1）由题意可得2c=2
，即c=，
又e=
=
，解得a=
，
b=
=1，
即有椭圆的方程为
+y2=1；
（2）由直线l过D（1，0）且垂直于x轴，设A（1，y1），B（1，﹣y1），
AE的方程为y﹣1=（1﹣y1）（x﹣2），令x=3可得M（3，2﹣y1），
即有BM的斜率为k=
=1
【解析】（1）由已知条件先求出椭圆C的半焦距，再由离心率公式和a，b，c的关系可得a，b，由此能求出椭圆C的标准方程；
（2）由直线l过D（1，0）且垂直于x轴，设A（1，y1），B（1，﹣y1），求得AE的方程，求得M的坐标，再由直线的斜率公式计算即可得到所求值.
练习册系列答案
相关题目
【题目】某工科院校对
， 
两个专业的男女生人数进行调查，得到如下的列联表：
专业 | 专业 | 总计 | |
女生 | 12 | 4 | 16 |
男生 | 38 | 46 | 84 |
总计 | 50 | 50 | 100 |
（Ⅰ）从
专业的女生中随机抽取2名女生参加某项活动，其中女生甲被选到的概率是多少？
（Ⅱ）能否有95%的把握认为工科院校中“性别”与“专业”有关系？
附：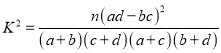 
．
|
|
|
|
|
|
|
|
|
|
|
|
