题目内容
设函数 .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)当 时,
时, 的最大值为2,求
的最大值为2,求 的值,并求出
的值,并求出 的对称轴方程.
的对称轴方程.
(1)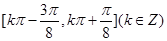 ;(2)
;(2) ,
, 的对称轴方程为
的对称轴方程为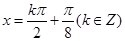 .
.
解析试题分析:(1)求函数 的单调递减区间,首先对
的单调递减区间,首先对 进行恒等变化,将它变为一个角的一个三角函数,然后利用三角函数的单调性,来求函数
进行恒等变化,将它变为一个角的一个三角函数,然后利用三角函数的单调性,来求函数 的单调递减区间,本题首先通过降幂公式降幂,及倍角公式,得到
的单调递减区间,本题首先通过降幂公式降幂,及倍角公式,得到 与
与 的关系式,再利用两角和的三角函数公式,得到
的关系式,再利用两角和的三角函数公式,得到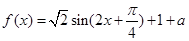 ,从而得到单调递增区间;(2)求
,从而得到单调递增区间;(2)求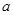 的值,由已知当
的值,由已知当 时,
时, 的最大值为2,由
的最大值为2,由 ,得
,得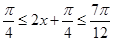 ,当
,当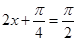 ,即
,即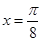 ,
,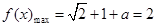 ,可求
,可求 的值,求
的值,求 的对称轴方程,即
的对称轴方程,即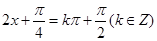 ,解出
,解出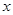 ,即得对称轴方程.
,即得对称轴方程.
试题解析:(1)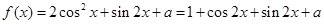
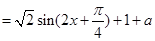 2分
2分
则 的最小正周期
的最小正周期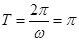 , 4分
, 4分
且当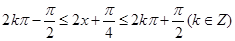 时
时 单调递增.
单调递增.
即 为
为 的单调递增区间
的单调递增区间
(写成开区间不扣分). 6分
(2)当 时
时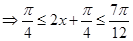 ,当
,当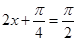 ,即
,即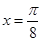 时
时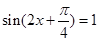 .
.
所以 . 9分
. 9分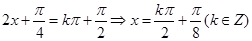 为
为 的对称轴. 12分
的对称轴. 12分
考点:二倍角的余弦;两角和与差的正弦函数;函数 的图象与性质.
的图象与性质.

练习册系列答案
相关题目
 ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b. 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围; ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A B,求实数m的取值范围.
B,求实数m的取值范围. ).
). )+2a+b,当x∈[0,
)+2a+b,当x∈[0, ]时,-5≤f(x)≤1.
]时,-5≤f(x)≤1. . 的部分图象如图所示,其中点
. 的部分图象如图所示,其中点 是图象的一个最高点.
是图象的一个最高点.
 的解析式;
的解析式; 且
且 ,求
,求 .
.
 的最小值.
的最小值.
 ;
; 是第三象限角,且
是第三象限角,且 ,求
,求 cos2ωx-
cos2ωx- 个单位长度,再将所得图象各点的横坐标缩小到原来的
个单位长度,再将所得图象各点的横坐标缩小到原来的 倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在
倍(纵坐标不变)得到函数y=g(x)的图象,求函数g(x)在 上的单调区间.
上的单调区间. ,钝角
,钝角 (角
(角 对边为
对边为 )的角
)的角 满足
满足 .
. 的单调递增区间;
的单调递增区间; ,求
,求 .
.