题目内容
已知α,β是关于x的二次方程2x2-tx-2=0的两个根,且α<β,若函数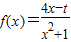 .
.(1)求
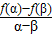 的值;
的值;(2)对任意x1,x2∈(α,β),求证:|f(x1)-f(x2)|<2|α-β|.
【答案】分析:(1)利用韦达定理,直接代入计算,可得结论;
(2)先证明函数在(α,β)上单调递增,再利用(1)的结论,即可得到结论.
解答:(1)解:由题意,α+β= ,αβ=-1,则t=2α+2β
,αβ=-1,则t=2α+2β
∴ =
= =
= =2×
=2×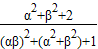 =2×
=2× =2×
=2× =2;
=2;
(2)证明:求导函数可得
∵x∈(α,β),∴2x2-tx-2<0,
∴-4x2+2tx+4>0,∴f′(x)>0
∴f(x)在(α,β)上单调递增
∴|f(x1)-f(x2)|<f(β)-f(α)
由(1)知,f(β)-f(α)=2(β-α)
∴|f(x1)-f(x2)|<2|α-β|.
点评:本题考查韦达定理的运用,考查不等式的证明,考查函数的单调性,考查学生的计算能力,属于中档题.
(2)先证明函数在(α,β)上单调递增,再利用(1)的结论,即可得到结论.
解答:(1)解:由题意,α+β=
 ,αβ=-1,则t=2α+2β
,αβ=-1,则t=2α+2β∴
 =
= =
= =2×
=2×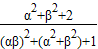 =2×
=2× =2×
=2× =2;
=2;(2)证明:求导函数可得

∵x∈(α,β),∴2x2-tx-2<0,
∴-4x2+2tx+4>0,∴f′(x)>0
∴f(x)在(α,β)上单调递增
∴|f(x1)-f(x2)|<f(β)-f(α)
由(1)知,f(β)-f(α)=2(β-α)
∴|f(x1)-f(x2)|<2|α-β|.
点评:本题考查韦达定理的运用,考查不等式的证明,考查函数的单调性,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目