题目内容
已知点F(1,0),直线L:x=-1,P为平面上的动点,过点P作直线L的垂线,垂足为Q,且
•
=
•
.
(1)求点P的轨迹C的方程;
(2)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有
•
<0?若存在,求出m的取值范围;若不存在,请说明理由.
| QP |
| QF |
| FP |
| FQ |
(1)求点P的轨迹C的方程;
(2)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有
| FA |
| FB |
分析:(1)设P的坐标为(x,y),则Q(-1,y),根据向量数量积的坐标运算公式,化简等式
•
=
•
,即可得到动点P的轨迹C的方程为y2=4x;
(2)设过点M的直线l方程为x=ty+m,直线l交曲线C于A(x1,y1),B(x2,y2).由直线l方程与曲线C方程消去x得关于y的一元二次方程,利用根与数的关系得
.根据
•
<0利用数量积的坐标运算,化简得x1x2-(x1-x2)+1+y1y2<0.根据曲线C的方程与前面得到的等式,化简得不等式m2-6m+1<4t2,从而得出m2-6m+1<0,解之得m的取值范围是(3-2
,3+2
).由此可得存在满足题中条件的正数m.
| QP |
| QF |
| FP |
| FQ |
(2)设过点M的直线l方程为x=ty+m,直线l交曲线C于A(x1,y1),B(x2,y2).由直线l方程与曲线C方程消去x得关于y的一元二次方程,利用根与数的关系得
|
| FA |
| FB |
| 2 |
| 2 |
解答:解:(1)设P的坐标为(x,y),则Q(-1,y),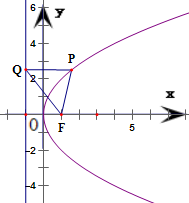 可得
可得
=(x+1,0),
=(2,-y),
=(x-1,y),
=(-2,y),
∵
•
=
•
,
∴(x+1)•2=(x-1)(-2)+y2,化简得y2=4x,
即动点P的轨迹C的方程为y2=4x.
(2)设l的方程为x=ty+m,过点M(m,0)(m>0)的直线l与
曲线C的交点为A(x1,y1),B(x2,y2).
由
消去x,得y2-4ty-4m=0.…(*)
则y1、y2是方程(*)的两根.
∴△=16(t2+m)>0,且
①
又∵
=(x1-1,y1),
=(x2-1,y2),
∴
•
<0,可得(x1-1)(x2-1)+y1y2<0,即x1x2-(x1-x2)+1+y1y2<0…②
由于x1x2=
•
,代入不等式②可得:
•
+y1y2-(
+
)+1<0,
化简得
+y1y2-
[(y1+y2)2-2y1y2]+1<0…③
由①式,化简不等式③得m2-6m+1<4t2,…④
对任意实数t,不等式4t2≥0恒成立,
∴不等式④对于一切t成立等价于m2-6m+1<0,
解之得3-2
<m<3+2
.
由此可得:存在正数m,对于过点M(m,0),且与曲线C有两个交点A,B的任一直线,
都有
•
<0,且m的取值范围是(3-2
,3+2
).
 可得
可得| QP |
| QF |
| FP |
| FQ |
∵
| QP |
| QF |
| FP |
| FQ |
∴(x+1)•2=(x-1)(-2)+y2,化简得y2=4x,
即动点P的轨迹C的方程为y2=4x.
(2)设l的方程为x=ty+m,过点M(m,0)(m>0)的直线l与
曲线C的交点为A(x1,y1),B(x2,y2).
由
|
则y1、y2是方程(*)的两根.
∴△=16(t2+m)>0,且
|
又∵
| FA |
| FB |
∴
| FA |
| FB |
由于x1x2=
| y12 |
| 4 |
| y22 |
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
化简得
(
| ||
| 16 |
| 1 |
| 4 |
由①式,化简不等式③得m2-6m+1<4t2,…④
对任意实数t,不等式4t2≥0恒成立,
∴不等式④对于一切t成立等价于m2-6m+1<0,
解之得3-2
| 2 |
| 2 |
由此可得:存在正数m,对于过点M(m,0),且与曲线C有两个交点A,B的任一直线,
都有
| FA |
| FB |
| 2 |
| 2 |
点评:本题着重考查了动点轨迹的求法、一元二次方程根与系数的关系、直线与抛物线的位置关系和向量数量积运算等知识,同时考查了逻辑思维能力、计算能力和转化化归的数学思想等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若