题目内容
 如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,若| QP |
| QF |
| FP |
| FQ |
(1)求动点P的轨迹C的方程;
(2)过点M(-1,0)作直线m交轨迹C于A,B两点.
(Ⅰ)记直线FA,FB的斜率分别为k1,k2,求k1+k2的值;
(Ⅱ)若线段AB上点R满足
| |MA| |
| |MB| |
| |RA| |
| |RB| |
分析:(1)设点P(x,y),则Q(-1,y),利用数量积
•
=
•
得:即可.
(2)(Ⅰ)由题意直线m斜率存在且不为0,设直线m:y=k(x+1)与抛物线方程联立,利用根与系数的关系和斜率计算公式即可得出k1+k2.
(Ⅱ)设动点R(x,y),利用
=
,即可得出x,进而即可证明RF⊥MF.
| QP |
| QF |
| FP |
| FQ |
(2)(Ⅰ)由题意直线m斜率存在且不为0,设直线m:y=k(x+1)与抛物线方程联立,利用根与系数的关系和斜率计算公式即可得出k1+k2.
(Ⅱ)设动点R(x,y),利用
| |MA| |
| |MB| |
| |RA| |
| |RB| |
解答:解:(1)设点P(x,y),则Q(-1,y),
由
•
=
•
得:(x+1,0)•(2,-y)=(x-1,y)•(-2,y),
化简得C:y2=4x.
(2)(Ⅰ)由题意直线m斜率存在且不为0,
设直线m:y=k(x+1)与抛物线方程联立
得k2x2+(2k2-4)x+k2=0
∵
,∴-1<k<1且k≠0.
设A(x1,y1),B(x1,y1)则x1+x2=
,x1x2=1.
∴k1+k2=
+
=
+
=k(2+
)=0.
(Ⅱ)设动点R(x,y),∵
=
,∴
=
,化为x=
=
=1.
∴R(1,yR),而F(1,0),∴
•
=(0,-yR)•(2,0)=0.
∴RF⊥MF.
由
| QP |
| QF |
| FP |
| FQ |
化简得C:y2=4x.
(2)(Ⅰ)由题意直线m斜率存在且不为0,
设直线m:y=k(x+1)与抛物线方程联立
|
得k2x2+(2k2-4)x+k2=0
∵
|
设A(x1,y1),B(x1,y1)则x1+x2=
| 4-2k2 |
| k2 |
∴k1+k2=
| y1 |
| x1-1 |
| y2 |
| x2-1 |
=
| k(x1+1) |
| x1-1 |
| k(x2+1) |
| x2-1 |
| 2(x1+x2)-4 |
| x1x2+1-(x1+x2) |
(Ⅱ)设动点R(x,y),∵
| |MA| |
| |MB| |
| |RA| |
| |RB| |
| x1+1 |
| x-x1 |
| x2+1 |
| x2-x |
| 2x1x2+x1+x2 |
| x1+x2+2 |
| 2+x1+x2 |
| x1+x2+2 |
∴R(1,yR),而F(1,0),∴
| RF |
| MF |
∴RF⊥MF.
点评:熟练掌握直线与抛物线相交问题转化为方程联立得到根与系数的关系、向量运算、数量积运算、斜率计算公式等是解题的关键.

练习册系列答案
相关题目
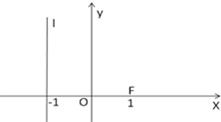 如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且
如图,已知点F(1,0),直线l:x=-1,P为平面上的动点,过P作直线l的垂线,垂足为点Q,且
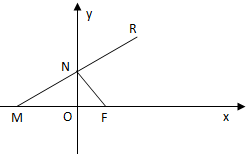 (2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且
(2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且 (2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且
(2006•嘉定区二模)如图,已知点F(1,0),点M在x轴上,点N在y轴上,且