Question

已知平面区域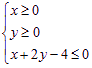恰好被面积最小的圆及其内部所覆盖． (Ⅰ)试求圆的方程；(Ⅱ)若斜率为1的直线与圆C交于点、，且，求直线的方程.

Answer 1

(Ⅰ)    (Ⅱ)

解析:

(1)由题意知此平面区域表示的是以构成的三角形及其内部,且△是直角三角形,             …………………………………3分

所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),半径是,………………4分

所以圆的方程是.    …………6分

   (2)设直线的方程是:.  ……………………………………………………7分

     因为,半径是,所以圆心到直线的距离是,   ………  8分

即    …10分解得:.  ………11分

所以直线的方程是:. ………………12分

另解：设直线的方程是:.  代人圆的方程是

整理得：

设，则

所以

所以

解得：

所以直线的方程是:.（参照给分）