题目内容
在数列{an}.中,如果对任意的n∈N,都有| an+2 |
| an+1 |
| an+1 |
| an |
①等比数列一定是比等差数列,等差数列不一定是比等差数列;
②如果{an}是等差数列,{bn}是等比数列,那么数列{anbn}是比等差数列:
③斐波那契数列{Fn}不是比等差数列;
④若an=2n-1•(n-1),则数列{an}为比等差数列,比公差e=2.
其中正确命题的序号是
分析:①根据等比数列的定义可知
=
,满足比等差数列的定义,若等差数列为an=n,看其是否满足;
②如果{an}是等差数列,{bn}是等比数列,设an=n,bn=2n,看其是否满足比等差数列的定义;
③斐波那契数列{Fn},根据斐波那契数列的性质进行化简变形,看其是否满足比等差数列的定义;
④若an=2n-1•(n-1),代入
-
进行求解看是否是常数,综合可得答案.
| an+2 |
| an+1 |
| an+1 |
| an |
②如果{an}是等差数列,{bn}是等比数列,设an=n,bn=2n,看其是否满足比等差数列的定义;
③斐波那契数列{Fn},根据斐波那契数列的性质进行化简变形,看其是否满足比等差数列的定义;
④若an=2n-1•(n-1),代入
| an+2 |
| an+1 |
| an+1 |
| an |
解答:解:①等比数列
-
=0,满足比等差数列的定义,若等差数列为an=n,则
-
=
≠常数,故正确;
②如果{an}是等差数列,{bn}是等比数列,设an=n,bn=2n,则
-
≠常数,不满足比等差数列的定义,故不正确;
③斐波那契数列{Fn},
-
=
-
≠常数,不满足比等差数列的定义,故正确;
④若an=2n-1•(n-1),
-
=
≠常数,不满足比等差数列的定义,故不正确;
故答案为:①③
| an+2 |
| an+1 |
| an+1 |
| an |
| an+2 |
| an+1 |
| an+1 |
| an |
| -1 |
| n(n+1) |
②如果{an}是等差数列,{bn}是等比数列,设an=n,bn=2n,则
| (n+2)2n+2 |
| (n+1)2n+1 |
| (n+1)2n+1 |
| n2n |
③斐波那契数列{Fn},
| an+2 |
| an+1 |
| an+1 |
| an |
| an+1+an |
| an+1 |
| an+an-1 |
| an |
④若an=2n-1•(n-1),
| an+2 |
| an+1 |
| an+1 |
| an |
| -1 |
| n(n-1) |
故答案为:①③
点评:本题考查新定义,解题时应正确理解新定义,同时注意利用列举法判断命题为假,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,an=3an-1+3n-1(n≥2,n∈N*).
,an=3an-1+3n-1(n≥2,n∈N*).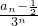 }是等差数列;
}是等差数列; ,an=3an-1+3n-1(n≥2,n∈N*).
,an=3an-1+3n-1(n≥2,n∈N*).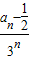 }是等差数列;
}是等差数列;