题目内容
在数列{an)中,已知a1=
,an=3an-1+3n-1(n≥2,n∈N*).
(1)求证:{
}是等差数列;
(2)求数列{an}的通项公式an及它的前n项和Sn.
| 7 |
| 2 |
(1)求证:{
an-
| ||
| 3n |
(2)求数列{an}的通项公式an及它的前n项和Sn.
分析:(1)利用数列递推式,结合
-
,即可证得结论;
(2)确定数列的通项,利用错位相减法可求数列的和.
an-
| ||
| 3n |
an-1-
| ||
| 3n-1 |
(2)确定数列的通项,利用错位相减法可求数列的和.
解答:(1)证明:∵an=3an-1+3n-1,
∴an-
=3(an-1-
)+3n,
∴
-
=
=1
∴{
}是等差数列,且公差为1;
(2)解:由(1){
}是等差数列,且公差为1,a1=
,
∴
=
+(n-1)×1=n,∴an=n•3n+
∴Sn=(1×31+2×32+…+n•3n)+
令Tn=1×31+2×32+…+n•3n,①则
3Tn=1×32+2×33+…+n•3n+1,②
①-②:-2Tn=31+32+…+3n-n•3n+1=-
(3-3n+1)-n•3n+1
∴Tn=
•3n+1+
∴Sn=
•3n+1+
+
∴an-
| 1 |
| 2 |
| 1 |
| 2 |
∴
an-
| ||
| 3n |
an-1-
| ||
| 3n-1 |
| an-3an-1+1 |
| 3n |
∴{
an-
| ||
| 3n |
(2)解:由(1){
an-
| ||
| 3n |
| 7 |
| 2 |
∴
an-
| ||
| 3n |
| ||||
| 3 |
| 1 |
| 2 |
∴Sn=(1×31+2×32+…+n•3n)+
| n |
| 2 |
令Tn=1×31+2×32+…+n•3n,①则
3Tn=1×32+2×33+…+n•3n+1,②
①-②:-2Tn=31+32+…+3n-n•3n+1=-
| 1 |
| 2 |
∴Tn=
| 2n-1 |
| 4 |
| 3 |
| 4 |
∴Sn=
| 2n-1 |
| 4 |
| 3 |
| 4 |
| n |
| 2 |
点评:本题考查数列递推式,考查等差数列的证明,考查数列的通项与求和,考查学生的计算能力,属于中档题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 ,an=3an-1+3n-1(n≥2,n∈N*).
,an=3an-1+3n-1(n≥2,n∈N*).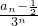 }是等差数列;
}是等差数列; ,an=3an-1+3n-1(n≥2,n∈N*).
,an=3an-1+3n-1(n≥2,n∈N*). }是等差数列;
}是等差数列; ,an=3an-1+3n-1(n≥2,n∈N*).
,an=3an-1+3n-1(n≥2,n∈N*).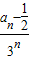 }是等差数列;
}是等差数列;