题目内容
4.在△ABC中,已知BC=2,$\frac{AB}{AC}$=$\frac{3}{4}$,sinC=$\frac{3\sqrt{15}}{16}$,求BC边上的中线AD的长.分析 首先利用余弦定理求出AC和AB的长度,然后在△ACD中利用余弦定理求出AD的长度.
解答 解:因为sinC=$\frac{3\sqrt{15}}{16}$,C是三角形的内角,所以cosC=$\frac{11}{16}$,设AB=3x,AC=4x,3x+4x>2,则$\frac{2}{7}$<x<2,
所以由余弦定理得到16x2+4-16x×$\frac{11}{16}$=9x2,解得x=1或x=$\frac{4}{7}$,
所以AB=3,AC=4或者AB=$\frac{3}{7}$,AC=$\frac{16}{7}$;
当AC=4时,在△ACD中,AD2=AC2+CD2-2AC×CDcosC=16+1-$\frac{11}{2}$=$\frac{23}{2}$,所以AD=$\frac{\sqrt{46}}{2}$;
当AC=$\frac{16}{7}$时,在△ACD中,AD2=AC2+CD2-2AC×CDcosC=$\frac{16}{49}+1-2×\frac{4}{7}×1×\frac{11}{16}$=$\frac{151}{49}$,所以AD=$\frac{\sqrt{151}}{7}$.
点评 本题主要考查了余弦定理在解三角形中的应用,关键是熟练运用余弦定理.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
14.已知{an}为等比数列,且a3•a9=2a52,a1=1,则a3=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
12.如图的程序框图表示求式子1×3×7×15×31×63的值,则判断框内可以填的条件为( )
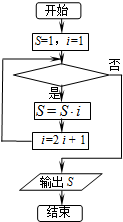

| A. | i≤31? | B. | i≤63? | C. | i≥63? | D. | i≤127? |
14.已知函数$f(x)=\sqrt{x}$和g(x)=alnx,曲线y=f(x)和y=g(x)有交点且在交点处有相同的切线,则a=( )
| A. | $\frac{e}{3}$ | B. | $\frac{e}{2}$ | C. | $\frac{2e}{3}$ | D. | e |
 有下列四个结论,
有下列四个结论,