题目内容
【题目】在平面直角坐标系xOy中,过点![]() 且互相垂直的两条直线分别与圆
且互相垂直的两条直线分别与圆![]() 交于点A,B,与圆
交于点A,B,与圆![]() 交于点C,D.
交于点C,D.

(1) 若AB=![]() ,求CD的长;
,求CD的长;
(2)若直线![]() 斜率为2,求
斜率为2,求![]() 的面积;
的面积;
(3) 若CD的中点为E,求△ABE面积的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]() .
.
【解析】
(1)分析直线斜率是否存在,当斜率存在时,利用圆中半弦长,半径,弦心距构成直角三角形求解即可(2)直线![]() 斜率为2,则直线
斜率为2,则直线![]() 方程为
方程为![]() ,求出弦长,点M到直线的距离,利用三角形面积公式求解即可(3)表示出△ABE的面积S=
,求出弦长,点M到直线的距离,利用三角形面积公式求解即可(3)表示出△ABE的面积S=![]() AB·d=2
AB·d=2![]() ,令
,令![]() ,换元后根据二次函数求最值即可.
,换元后根据二次函数求最值即可.
(1) 由题可知,直线AB斜率显然存在,设为k,则直线AB:y=kx+1.
因为O点到直线AB的距离d1=![]() ,
,
∴![]() +
+![]() =4,
=4,
∴AB=2![]()
由2![]() =
=![]() 得k2=15.
得k2=15.
因为直线AB与直线CD互相垂直,则直线CD:y=![]() x+1,
x+1,
∴M点到直线CD的距离d2=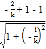 ,
,
∴![]() =1-
=1-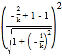 ,CD=2
,CD=2![]() =2
=2![]() =
=![]() .
.
(2) 直线![]() 斜率为2,则直线
斜率为2,则直线![]() 方程为
方程为![]()
![]() 到直线
到直线![]() 距离为
距离为![]() 到直线
到直线![]() 距离为
距离为![]()
![]()
![]()
(3)当直线AB的斜率不存在时,△ABE的面积S=![]() ×4×2=4;
×4×2=4;
当直线AB的斜率存在时,设为k,则直线AB:y=kx+1,k≠0,直线CD:y=-![]() x+1.
x+1.
由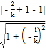 <1得k2>3, 所以k∈(-∞,-
<1得k2>3, 所以k∈(-∞,-![]() )∪(
)∪(![]() ,+∞).
,+∞).
因为![]() +
+![]() =4,所以AB=2
=4,所以AB=2![]() .
.
因为E点到直线AB的距离即M点到直线AB的距离d=![]() =
=![]() ,
,
所以△ABE的面积S=![]() AB·d=2
AB·d=2![]() .
.
令![]() ,则S=
,则S=![]()
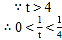
![]() ∈
∈![]() .
.
综上,△ABE面积的取值范围是![]() .
.

【题目】某气象站观测点记录的连续4天里,AQI指数M与当天的空气水平可见度y(单位cm)的情况如下表1:
M | 900 | 700 | 300 | 100 |
y | 0.5 | 3.5 | 6.5 | 9.5 |
哈尔滨市某月AQI指数频数分布如下表2:
M | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设x= ![]() ,根据表1的数据,求出y关于x的回归方程; (参考公式:
,根据表1的数据,求出y关于x的回归方程; (参考公式: ![]() ;其中
;其中 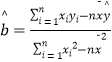 ,
, ![]() )
)
(2)小张开了一家洗车店,经统计,当M不高于200时,洗车店平均每天亏损约2000元;当M在200至400时,洗车店平均每天收入约4000元;当M大于400时,洗车店平均每天收入约7000元;根据表2估计小张的洗车店该月份平均每天的收入.
