题目内容
已知集合A={y|y2-(a2+a+1)y+a(a2+1)>0},B={y|y=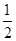 x2-x+
x2-x+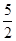 ,0≤x≤3}.
,0≤x≤3}.
(1)若A∩B=∅,求a的取值范围;
(2)当a取使不等式x2+1≥ax恒成立的a的最小值时,求(∁RA)∩B.
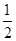 x2-x+
x2-x+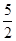 ,0≤x≤3}.
,0≤x≤3}.(1)若A∩B=∅,求a的取值范围;
(2)当a取使不等式x2+1≥ax恒成立的a的最小值时,求(∁RA)∩B.
(1)(-∞,- ]∪[
]∪[ ,2]
,2]
(2){y|2≤y≤4}
 ]∪[
]∪[ ,2]
,2](2){y|2≤y≤4}
A={y|y<a或y>a2+1},B={y|2≤y≤4}.
(1)当A∩B=∅时,
∴ ≤a≤2或a≤-
≤a≤2或a≤- .
.
∴a的取值范围是(-∞,- ]∪[
]∪[ ,2].
,2].
(2)由x2+1≥ax,得x2-ax+1≥0,
依题意Δ=a2-4≤0,
∴-2≤a≤2.
∴a的最小值为-2.
当a=-2时,A={y|y<-2或y>5}.
∴∁RA={y|-2≤y≤5}.
∴(∁RA)∩B={y|2≤y≤4}.
(1)当A∩B=∅时,

∴
 ≤a≤2或a≤-
≤a≤2或a≤- .
.∴a的取值范围是(-∞,-
 ]∪[
]∪[ ,2].
,2].(2)由x2+1≥ax,得x2-ax+1≥0,
依题意Δ=a2-4≤0,
∴-2≤a≤2.
∴a的最小值为-2.
当a=-2时,A={y|y<-2或y>5}.
∴∁RA={y|-2≤y≤5}.
∴(∁RA)∩B={y|2≤y≤4}.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 ,则实数a的取值范围是( )
,则实数a的取值范围是( )



 ,且
,且 ,则实数
,则实数 的取值范围是 .
的取值范围是 . ,
, ,则( )
,则( )



 ,则集合
,则集合 ( )
( )



 ,集合
,集合 ,则
,则 =( )
=( )



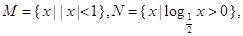 则
则 为( )
为( )


