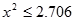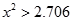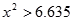题目内容
设有关于 的一元二次方程
的一元二次方程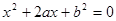
(1)若 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,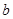 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若 是从区间[0,3]任取的一个数,
是从区间[0,3]任取的一个数,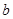 是从区间[0,2]任取的一个数,求上述方程有实根的概率.
是从区间[0,2]任取的一个数,求上述方程有实根的概率.
(1)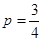 (2)
(2)
解析试题分析:(1)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(2)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;(3)注意判断是古典概型还是几何概型,基本事件前者是有限的,后者是无限的,两者都是等可能性.(4)在几何概型中注意区域是线段,平面图形,立体图形.
试题解析:解:设事件A为“方程x2+2ax+b2=0有实根”.
当a≥0,b≥0时,方程x2+2ax+b2=0有实根的充要条件为a≥b.
(1)基本事件共有12个:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).其中第一个数表示a的取值,第二个数表示b的取值.事件A中包含9个基本事件,事件A发生的概率为P(A)=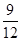 =
= ..6分
..6分
(2)试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2},构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b},所以所求的概率为P(A)=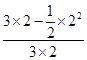 =
=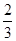 12分
12分
考点:(1)古典概型的概率; (2)几何概型的概率.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案某同学在生物研究性学习中想对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
| 日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差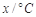 | 10 | 11 | 13 | 12 | 8 |
发芽数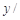 颗 颗 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为
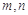 ,求事件“
,求事件“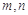 均不小于25的概率。
均不小于25的概率。(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出
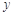 关于
关于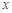 的线性回归方程
的线性回归方程 ;
;(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?(参考公式:
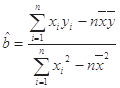 ,
,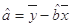 )
)  是以
是以 为圆心,半径为1的圆的内接正方形,将一颗豆子随机
为圆心,半径为1的圆的内接正方形,将一颗豆子随机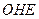 (阴影部分)内”,则(1)
(阴影部分)内”,则(1)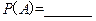 ;(2)
;(2)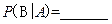

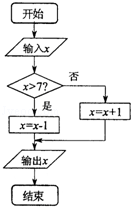
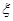 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 列联表:
列联表: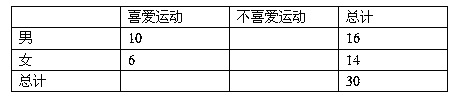
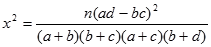 (其中
(其中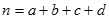 )
)