题目内容
某县为增强市民的环境保护意识,面向全县征召义务宣传志愿者,先从符合条件的志愿者中随机抽取100名按年龄分组:第1组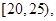 第2组
第2组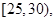 第3组
第3组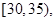 第4组
第4组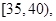 第5组
第5组 得到的频率分布直方图如图所示,
得到的频率分布直方图如图所示,
(1)分别求第3,4,5组的频率。
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参与广场的宣传活动,应从第3,4,5组各抽取多少名志愿者.
(3)在(2)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.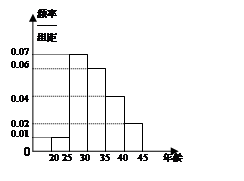
(1)0.3,0.2,0.1;(2)第3,4,5组中分别抽取3名,2名,1名志愿者;(3) .
.
解析试题分析:
解题思路:(1)根据各个矩形的面积是频率求解;(2)利用分层抽样的特点“等比例抽样”求解;
(3)列举基本事件,利用古典概型概率公式求解.
规律总结:以图表给出的统计题目一般难度不大,主要考查频率直方图、茎叶图、频率分布表给出;抽样方法要注意各自的特点;古典概型是一种重要的概率模型,其关键是正确列举基本事件.
试题解析:(1)由题设可知,第3组的频率为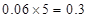 ,第4组的频率为
,第4组的频率为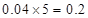 ,第5组的频率为
,第5组的频率为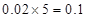 .
.
(2)第3组的人数为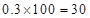 ,第4组的人数为
,第4组的人数为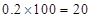 ,
,
第5组的人数为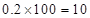 。因为第3,4,5组共有60名志愿者,若利用分层抽样的方法在60名志愿者中抽取6名志愿者,则每组抽取的人数分别为:第3组为
。因为第3,4,5组共有60名志愿者,若利用分层抽样的方法在60名志愿者中抽取6名志愿者,则每组抽取的人数分别为:第3组为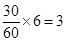 ,第4组为
,第4组为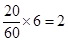 ,第5组为
,第5组为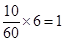 .所以应从第3,4,5组中分别抽取3名,2名,1名志愿者.
.所以应从第3,4,5组中分别抽取3名,2名,1名志愿者.
(3)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,第5组的一名志愿者为C。
则从6名志愿者中抽取2名志愿者的可能情况有:(A1,A2),
(A1,A3),(A1,B1),(A1,B2),(A1,C),(A2,A3),(A2,B1),(A2,B2),(A2,C),(A3,B1),(A3,B2),(A3,C),(B1,B2),(B1,C)(B2,C),共15种。
其中第4组的2名志愿者至少有一名志愿者被抽中的可能情况有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),(B1,C)(B2,C),共9种.
所以第4组至少有一名志愿者被抽中的概率为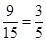 .
.
考点:1.频率分布直方图;2.分层抽样;3.古典概型.

吸烟的危害很多,吸烟产生的烟雾中有近2000种有害物质,如尼古丁、氰氢酸、氨、一氧化碳、二氧化碳、吡啶、砷、铜、铅等,还有40多种致癌物,如苯并芘、朕苯胺及煤焦油等。它们随吸烟者吞咽烟雾时进入体内,对机体产生危害。为了解某市心肺疾病是否与吸烟有关,某医院随机对入院的50人进行了问卷调查,得到了如下的列联表.
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 吸烟患者 | 20 | 5 | 25 |
| 不吸烟患者 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(1)用分层抽样的方法在患心肺疾病的人群中抽3人,其中吸烟患者抽到多少人?
(2)在上述抽取的3人中选2人,求恰有一名不吸烟患者的概率;
(3)是否有99.5%的把握认为患心肺疾病与吸烟有关?
附:
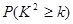 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:
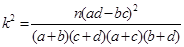 ,其中
,其中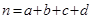
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
| 日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
②若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
 ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.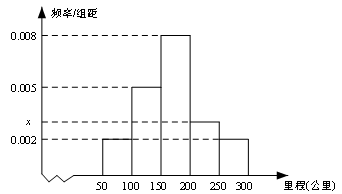
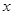 的值;
的值;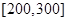 的车辆数;
的车辆数;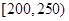 的概率.
的概率.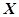 为取得红球的个数.
为取得红球的个数.