题目内容
红队队员甲、乙与蓝队队员A、B进行围棋比赛,甲对A、乙对B各比一盘.已知甲胜A,乙胜B的概率分别为0.6、0.5.假设各盘比赛结果相互独立.
(1)求红队至少一名队员获胜的概率;
(2)用ξ表示红队队员获胜的总盘数,求ξ的分布列.
(1)0.8;(2)ξ 0 1 2 P 0.2 0.5 0.3
解析试题分析:(1)设甲获胜的事件为D,乙获胜的事件为E,则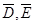 分别为甲不胜、乙不胜的事件,P(D)=0.6,P(E)=0.5,由此能求出红队至少有一人获胜的概率.
分别为甲不胜、乙不胜的事件,P(D)=0.6,P(E)=0.5,由此能求出红队至少有一人获胜的概率.
(2)由题意知ξ可能的取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列.
试题解析:(1)设甲获胜的事件为D,乙获胜的事件为E,
则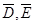 分别为甲不胜、乙不胜的事件,
分别为甲不胜、乙不胜的事件,
∵P(D)=0.6,P(E)=0.5,∴P(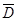 )=0.4,P(
)=0.4,P(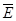 )=0.5,
)=0.5,
红队至少有一人获胜的概率为:
P=P(D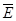 )+P(
)+P(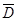 E)+P(DE)
E)+P(DE)
=0.6×0.5+0.4×0.5+0.6×0.5=0.8.
(2)由题意知ξ可能的取值为0,1,2,
又由(1)知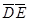 ,D
,D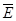 ,
,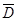 E,DE两两互斥,且各盘比赛的结果相互独立,
E,DE两两互斥,且各盘比赛的结果相互独立,
∴P(ξ=0)=P(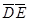 )=0.4×0.5=0.2,
)=0.4×0.5=0.2,
P(ξ=1)=P(D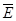 )+P(
)+P(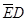 )=0.6×0.5+0.4×0.5=0.5,
)=0.6×0.5+0.4×0.5=0.5,
P(ξ=2)=0.6×0.5=0.3,
∴ξ的分布列为:
考点:1.概率的求法;2.离散型随机变量的分布列的求法.ξ 0 1 2 P 0.2 0.5 0.3

练习册系列答案
相关题目
某企业主要生产甲、乙两种品牌的空调,由于受到空调在保修期内维修费等因素的影响,企业生产每台空调的利润与该空调首次出现故障的时间有关,甲、乙两种品牌空调的保修期均为3年,现从该厂已售出的两种品牌空调中各随机抽取50台,统计数据如下:
| 品牌 | 甲 | 乙 | |||||
| 首次出现故障时间 x年 |  |  |  |  |  |  |  |
| 空调数量(台) | 1 | 2 | 4 | 43 | 2 | 3 | 45 |
| 每台利润(千元) | 1 | 2 | 2.5 | 2.7 | 1.5 | 2.6 | 2.8 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌空调中随机抽取一台,求首次出现故障发生在保修期内的概率;
(2)若该厂生产的空调均能售出,记生产一台甲品牌空调的利润为X1,生产一台乙品牌空调的利润为X2,分别求X1,X2的分布列;
(3)该厂预计今后这两种品牌空调销量相当,但由于资金限制,只能生产其中一种品牌空调,若从经济效益的角度考虑,你认为应该生产哪种品牌的空调?说明理由。
 ,若
,若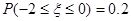 ,则
,则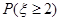 等于 .
等于 .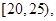 第2组
第2组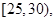 第3组
第3组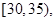 第4组
第4组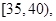 第5组
第5组 得到的频率分布直方图如图所示,
得到的频率分布直方图如图所示,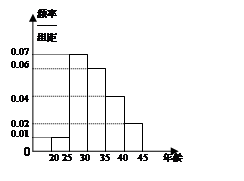
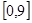 上随机取一实数
上随机取一实数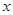 ,则该实数
,则该实数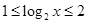 的概率为 .
的概率为 .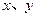 的取值如下表所示:
的取值如下表所示: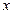

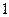
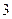
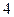
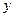
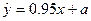 ,则
,则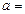 ______
______