题目内容
【题目】设函数![]() .
.
(![]() )求数
)求数![]() 的最小正周期和对称轴方程.
的最小正周期和对称轴方程.
(![]() )锐角
)锐角![]() 的三个顶点
的三个顶点![]() ,
, ![]() ,
, ![]() 所对边分别为
所对边分别为![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 及边
及边![]() .
.
(![]() )若
)若![]() 中,
中, ![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(![]() )
)![]() 对称轴方程:
对称轴方程: ![]() (
(![]() )
)![]() ,
, ![]() (
(![]() )
)![]()
【解析】试题分析:(1)利用诱导公式、和差化积公式、积化和差公式进行计算得到![]() ,据此求得其最小正周期和单调区间;(2)利用(1)的结论得到
,据此求得其最小正周期和单调区间;(2)利用(1)的结论得到
![]() ,易得
,易得![]() ,由正弦定理得到:sinB=
,由正弦定理得到:sinB=![]() ,结合角B的取值范围和特殊角的三角函数值推知角B的大小,利用三角形内角和定理可以求得角C的大小,所以由余弦定理来求c的值即可.(3)
,结合角B的取值范围和特殊角的三角函数值推知角B的大小,利用三角形内角和定理可以求得角C的大小,所以由余弦定理来求c的值即可.(3)![]() ,∴
,∴![]() 或
或![]() ,在
,在![]() 中,
中, ![]() ,化简
,化简![]() ,解出A的范围再求出原式的范围.
,解出A的范围再求出原式的范围.
试题解析:
(![]() )∵
)∵![]()
![]() ,
,
![]() ,
,
![]() .
.
![]() 最小正周期
最小正周期![]() ,对称轴方程:
,对称轴方程: ![]() ,
,
![]() .
.
(![]() )∵
)∵![]() ,∴
,∴![]() ,
, ![]() ,
,
又∵![]() 是锐角三角形,∴
是锐角三角形,∴![]() ,又∵
,又∵![]() ,
, ![]() ,
, ![]() ,
,
解出![]() 或
或![]() .又∵由正弦定理
.又∵由正弦定理![]() ,∴
,∴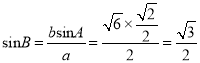 ,
,
∴在锐角![]() 中,
中, ![]() ,∴
,∴![]() ,∵在
,∵在![]() 中,
中, ![]() ,
,
∴![]() ,∴
,∴![]() .
.
综上, ![]() ,
, ![]() .
.
(![]() )∵
)∵![]() ,
, ![]() ,∴
,∴![]() 或
或![]() ,
,
在![]() 中,
中, ![]() ,又∵
,又∵![]()
![]() ,
,
![]() .
.
令![]() ,
,
原式![]()
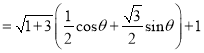 ,
,
![]() ,
,
![]() .
.
∵在![]() 中,
中, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
,
代入不等式,解出![]() .∴
.∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() .
.
所以原式的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别 | 男 | 女 | 总计 |
中年组 |
|
| 91 |
老年组 | 16 |
|
|
已知中年组女性选手人数是仅比老年组女性选手人数多2人,若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(1)求表格中的数据![]() ;
;
(2)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.