题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 在
在 ![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,当
,当![]() 时,求
时,求![]() 的最小值;
的最小值;
(3)求证:![]() .
.
【答案】(1) 实数![]() 的值为
的值为![]() ;(2) 当
;(2) 当![]() 时,
时,![]() 的最小值为
的最小值为![]() 当
当![]() 时,
时, ![]() 的最小值为
的最小值为![]() 当
当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ;(3)证明如下.
;(3)证明如下.
【解析】
(1)求出切点纵坐标即可求解;
(2)先求函数![]() 的单调性,再讨论所给的动区间的位置即可得出;
的单调性,再讨论所给的动区间的位置即可得出;
(3)对所要证明的不等式两边取对数,构造函数转化为恒成立问题即可证明.
(1) 由题意可知,![]() .
.
(2) ![]() 令
令![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 的最小值为
的最小值为![]()
当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 的最小值为
的最小值为![]()
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() 的最小值为
的最小值为![]() .
.
综上所述,当![]() 时,
时,![]() 的最小值为
的最小值为![]()
当![]() 时,
时, ![]() 的最小值为
的最小值为![]()
当![]() 时,
时, ![]() 的最小值为
的最小值为![]() .
.
(3)要证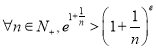 ,即证
,即证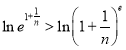 ,
,
只需证![]() ,即证
,即证![]() 对任意的
对任意的![]() 恒成立.
恒成立.
令![]() 则
则![]() ,当
,当![]() 时,
时,![]() 恒成立,
恒成立,
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上的最大值为
上的最大值为![]() ,
,
即![]() 对任意的
对任意的![]() 恒成立,
恒成立,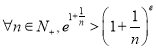 得证.
得证.

练习册系列答案
相关题目
【题目】千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,观察了所在地区A的100天日落和夜晚天气,得到如下![]() 列联表:
列联表:
夜晚天气 日落云里走 | 下雨 | 未下雨 |
出现 | 25 | 5 |
未出现 | 25 | 45 |
临界值表 | ||||
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并计算得到![]() ,下列小波对地区A天气判断不正确的是( )
,下列小波对地区A天气判断不正确的是( )
A.夜晚下雨的概率约为![]()
B.未出现“日落云里走”夜晚下雨的概率约为![]()
C.有![]() 的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
的把握认为“‘日落云里走’是否出现”与“当晚是否下雨”有关
D.出现“日落云里走”,有![]() 的把握认为夜晚会下雨
的把握认为夜晚会下雨