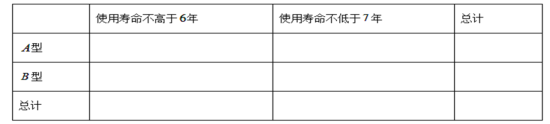
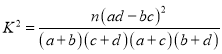题目内容
【题目】已知函数f(x)=ex(x﹣2)![]() ax2+ax(a∈R).
ax2+ax(a∈R).
(1)当a=1时,求f(x)的极值;
(2)若f(x)恰有两个零点,求实数a的取值范围.
【答案】(1)f(x)极大值=﹣2,f(x)极小值=![]() ﹣e;(2)a∈(﹣∞,0)∪{2e}.
﹣e;(2)a∈(﹣∞,0)∪{2e}.
【解析】
(1)代入a的值,求出函数的导数,解关于导函数的不等式,求出函数的极值即可;
(2)显然x=2是函数f(x)的一个零点,若f(x)恰有两个零点,则只需y=ex![]() ax恰有1个零点,问题转化为只需g(x)=ex和h(x)
ax恰有1个零点,问题转化为只需g(x)=ex和h(x)![]() ax只有1个交点即可,通过讨论a的范围,结合函数的图象判断即可.
ax只有1个交点即可,通过讨论a的范围,结合函数的图象判断即可.
(1)a=1时,f(x)=ex(x﹣2)![]() x2+x,
x2+x,
f′(x)=ex(x﹣1)﹣x+1=(x﹣1)(ex﹣1),
令f′(x)>0,解得:x>1或x<0,
令f′(x)<0,解得:0<x<1,
故f(x)在(﹣∞,0)递增,在(0,1)递减,在(1,+∞)递增,
故f(x)极大值=f(0)=﹣2,f(x)极小值=f(1)=![]() ﹣e.
﹣e.
(2)f(x)=ex(x﹣2)![]() ax2+ax=(x﹣2)(ex
ax2+ax=(x﹣2)(ex![]() ax),
ax),
显然x=2是函数f(x)的一个零点,若f(x)恰有两个零点,
则只需y=ex![]() ax恰有1个零点,
ax恰有1个零点,
即只需g(x)=ex和h(x)![]() ax只有1个交点即可,
ax只有1个交点即可,
①a<0时,如图示:
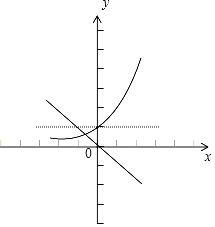
结合图象,a<0时g(x)=ex和h(x)![]() ax只有1个交点,符合题意;
ax只有1个交点,符合题意;
②a=0时,g(x)=ex和y=0无交点,不合题意;
③a>0时,g(x)=ex和h(x)![]() ax相切时1个交点,
ax相切时1个交点,
设切点是P(m,em),则![]() a=em(i),
a=em(i),
em![]() am(ii),由(i)(ii)解得:P(1,e),a=2e,符合题意,
am(ii),由(i)(ii)解得:P(1,e),a=2e,符合题意,
综上,若f(x)恰有两个零点,则a∈(﹣∞,0)∪{2e}.

【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中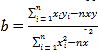 ,
,![]() .
.
【题目】健身馆某项目收费标准为每次60元,现推出会员优惠活动:具体收费标准如下:
消费次数 | 第1次 | 第2次 | 第3次 | 不少于4次 |
收费比例 | 0.95 | 0.90 | 0.85 | 0.80 |
现随机抽取了100位会员统计它们的消费次数,得到数据如下:
消费次数 | 1次 | 2次 | 3次 | 不少于4次 |
频数 | 60 | 25 | 10 | 5 |
假设该项目的成本为每次30元,根据给出的数据回答下列问题:
(1)估计1位会员至少消费两次的概率
(2)某会员消费4次,求这4次消费获得的平均利润;