题目内容
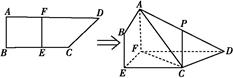
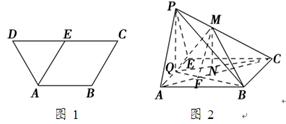
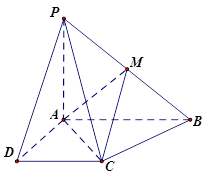
已知四棱锥 的底面为直角梯形,
的底面为直角梯形,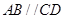 ,
, ,
,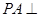 底面
底面 ,且
,且 ,
, 是
是 的中点.
的中点.
⑴求证:直线 平面
平面 ;
;
⑵若直线 与平面
与平面 所成的角为
所成的角为 ,求四棱锥
,求四棱锥 的体积.
的体积.
⑴见解析;⑵1
解析试题分析:⑴要证直线 平面
平面 ,需要在平面
,需要在平面 内找到一条与
内找到一条与 平行的直线.显然不容易找到;故考虑利用面面平行退出线面平行, 取
平行的直线.显然不容易找到;故考虑利用面面平行退出线面平行, 取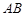 的中点
的中点 ,构造平面
,构造平面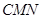 ,根据
,根据 ,
, ∥
∥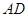 可证.
可证.
⑵利用体积公式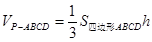 .需求出梯形
.需求出梯形 的面积,根据
的面积,根据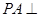 底面
底面 ,可知
,可知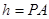 .
.
试题解析:⑴证明:取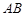 的中点
的中点 ,则
,则 ,故
,故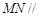 平面
平面 ;
;
又四边形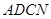 正方形,∴
正方形,∴ ∥
∥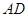 ,故
,故 ∥平面
∥平面 ;
;
∴平面 平面
平面 ,
,
∴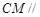 平面
平面 .
.
⑵根据⑴可知, 平面
平面 .所以根据题意有
.所以根据题意有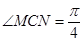 ;
;
因为四边形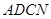 为正方形,所以
为正方形,所以 为等腰直角三角形.所以
为等腰直角三角形.所以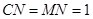 ,
,
根据 可知
可知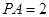 ,又因为
,又因为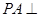 底面
底面 ,所以棱锥的高为
,所以棱锥的高为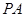 .
.
因为梯形 的面积为
的面积为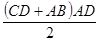 ,故
,故 .
.
考点:利用面面平行证明线面平行;棱锥体积;

练习册系列答案
相关题目
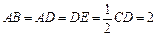 ,M是线段AE上的动点.
,M是线段AE上的动点.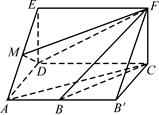
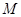 是母线
是母线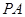 的中点,
的中点,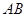 是底面圆的直径,半径
是底面圆的直径,半径 与母线
与母线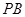 所成的角的大小等于
所成的角的大小等于 .
.
 与
与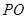 所成的角;
所成的角; A′B′C′,∠BAC=90°,AB=AC=
A′B′C′,∠BAC=90°,AB=AC= ,AA′=1,点M,N分别为
,AA′=1,点M,N分别为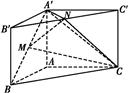
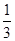 Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高)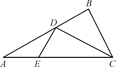 图①
图①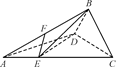 图②
图②