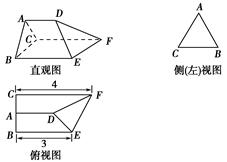
题目内容
如图,直三棱柱ABC A′B′C′,∠BAC=90°,AB=AC=
A′B′C′,∠BAC=90°,AB=AC= ,AA′=1,点M,N分别为
,AA′=1,点M,N分别为
A′B和B′C′的中点.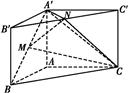
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′ MNC的体积.(锥体体积公式V=
MNC的体积.(锥体体积公式V=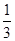 Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高)
(1)见解析 (2)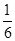
解析(1)证明:法一 连接AB′,AC′,如图所示,由已知∠BAC=90°,AB=AC,三棱柱ABC A′B′C′为直三棱柱,
A′B′C′为直三棱柱,
所以M为AB′的中点.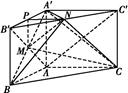
又因为N为B′C′的中点,
所以MN∥AC′.
又MN?平面A′ACC′,AC′?平面A′ACC′,
所以MN∥平面A′ACC′.
法二 取A′B′的中点P,连接MP,NP,AB′,如图所示,
因为M,N分别为AB′与B′C′的中点,
所以MP∥AA′,PN∥A′C′.
所以MP∥平面A′ACC′,PN∥平面A′ACC′.
又MP∩NP=P,所以平面MPN∥平面A′ACC′.
而MN?平面MPN,所以MN∥平面A′ACC′.
(2)解:连接BN,如图所示,
由题意知A′N⊥B′C′,平面A′B′C′∩平面B′BCC′=B′C′,
所以A′N⊥平面NBC.
又A′N= B′C′=1,
B′C′=1,
故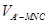 =
=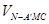 =
=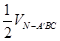 =
=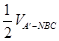 =
=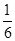 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是圆柱体的轴截面,
是圆柱体的轴截面, 分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为
分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为 ,且该圆柱体的体积为
,且该圆柱体的体积为 ,如图所示.
,如图所示.
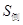 的值;
的值; 是半圆弧
是半圆弧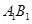 的中点,点
的中点,点 在半径
在半径 上,且
上,且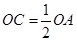 ,异面直线
,异面直线 与
与 所成的角为
所成的角为 ,求
,求 的值.
的值.
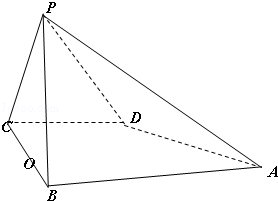
 ,求三棱锥A一BCD的体积.
,求三棱锥A一BCD的体积. ,底面
,底面 是等腰梯形,且
是等腰梯形,且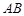 ∥
∥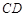 ,
, 是
是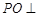 平面
平面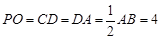 ,
, 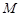 是
是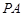 中点.
中点.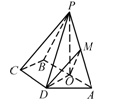
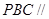 平面
平面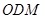 ;(2)求点
;(2)求点 到平面
到平面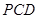 的距离.
的距离. 的底面为直角梯形,
的底面为直角梯形,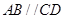 ,
, ,
,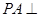 底面
底面 ,且
,且 ,
, 是
是 的中点.
的中点. 平面
平面 ;
; 与平面
与平面 所成的角为
所成的角为 ,求四棱锥
,求四棱锥