题目内容
自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在的直线方程.
4x+3y+3=0或3x+4y-3=0
【错解分析】设反射光线为L′,由于L和L′关于x轴对称,L过点A(-3,3),点A关于x轴的对称点A′(-3,-3),于是L′过A(-3,-3). 设L′的斜率为k,则L′的方程为y-(-3)=k[x-(-3)],即kx-y+3k-3=0,已知圆方程即(x-2)2+(y-2)2=1,圆心O的坐标为(2,2),半径r=1因L′和已知圆相切,则O到L′的距离等于半径r=1 即
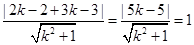 整理得12k2-25k+12=0
整理得12k2-25k+12=0解得k=
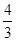 L′的方程为y+3=
L′的方程为y+3=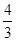 (x+3) 即4x-3y+3=0 因L和L′关于x轴对称故L的方程为4x+3y+3=0.
(x+3) 即4x-3y+3=0 因L和L′关于x轴对称故L的方程为4x+3y+3=0.【正解】设反射光线为L′,由于L和L′关于x轴对称,L过点A(-3,3),点A关于x轴的对称点A′(-3,-3), 于是L′过A(-3,-3). 设L′的斜率为k,则L′的方程为y-(-3)=k[x-(-3)],即kx-y+3k-3=0, 已知圆方程即(x-2)2+(y-2)2=1,圆心O的坐标为(2,2),半径r=1
因L′和已知圆相切,则O到L′的距离等于半径r=1
即
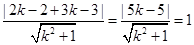 整理得12k2-25k+12=0 解得k=
整理得12k2-25k+12=0 解得k=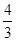 或k=
或k=
L′的方程为y+3=
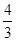 (x+3);或y+3=
(x+3);或y+3= (x+3)。 即4x-3y+3=0或3x-4y-3=0
(x+3)。 即4x-3y+3=0或3x-4y-3=0因L和L′关于x轴对称故L的方程为4x+3y+3=0或3x+4y-3=0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
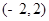 ,半径为5的圆的标准方程为( )
,半径为5的圆的标准方程为( )



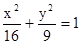 上一点, F1、F2是其焦点, 若∠F1P F2=90°, △F1P F2面积为 .
上一点, F1、F2是其焦点, 若∠F1P F2=90°, △F1P F2面积为 . 
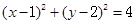 关于
关于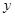 轴对称的圆的方程为______________.
轴对称的圆的方程为______________. 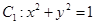 ,圆
,圆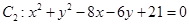 ,则两圆公切线的条数有( )
,则两圆公切线的条数有( )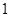 条
条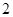 条
条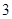 条
条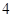 条
条 上的点到直线
上的点到直线 的最小距离是 .
的最小距离是 .