题目内容
(本小题满分12分)
己知圆C: (x – 2 )2 + y 2 =" 9," 直线l:x + y = 0.
(1) 求与圆C相切, 且与直线l平行的直线m的方程;
(2) 若直线n与圆C有公共点,且与直线l垂直,求直线n在y轴上的截距b的取值范围;
己知圆C: (x – 2 )2 + y 2 =" 9," 直线l:x + y = 0.
(1) 求与圆C相切, 且与直线l平行的直线m的方程;
(2) 若直线n与圆C有公共点,且与直线l垂直,求直线n在y轴上的截距b的取值范围;
(1) x + y – 2 +3 ="0," 或x + y – 2 –3
="0," 或x + y – 2 –3 ="0" (2)
="0" (2) 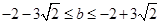
 ="0," 或x + y – 2 –3
="0," 或x + y – 2 –3 ="0" (2)
="0" (2) 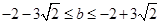
试题分析:(1) ∵直线m∥直线x + y = 0,
∴设m: x + y + c = 0,
∵直线m与圆C相切,∴ 3 =
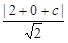 ,
,解得 c =" –" 2 ±3
 ,
,所以所求直线m的方程为:x + y – 2 +3
 ="0," 或x + y – 2 –3
="0," 或x + y – 2 –3 ="0."
="0." (2) 由条件设直线n的方程为:y = x +b ,
代入圆C方程整理得:2x2 +2 (b – 2)x + b2 – 5 = 0,
∵直线l与圆C有公共点,
∴△ =" 4(b" – 2)2 – 8(b2 – 5 ) =" –" 4b2 – 16b +56 ≥ 0,
即:b2 + 4b –14 £ 0
解得:
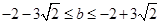 .
.点评:直线与圆的位置关系问题,一般用圆心到直线的距离与半径之间的关系解决,这种方法比联立方程组简单.

练习册系列答案
相关题目
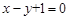 上,且经过圆
上,且经过圆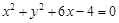 与圆
与圆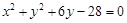 的交点的圆方程.
的交点的圆方程.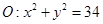 ,椭圆
,椭圆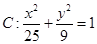 .
.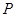 在圆
在圆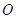 上,线段
上,线段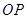 的垂直平分线经过椭圆的右焦点,求点
的垂直平分线经过椭圆的右焦点,求点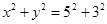 上任意一点
上任意一点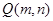 作椭圆
作椭圆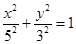 的两条切线,则这两条切线互相垂直”;
的两条切线,则这两条切线互相垂直”;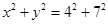 上任意一点
上任意一点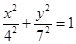 的两条切线,则这两条切线互相垂直”.
的两条切线,则这两条切线互相垂直”. 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 为切点,
为切点, .若
.若 ,
, ,则
,则 的长为 .
的长为 . 
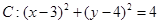 和直线
和直线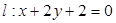 ,直线
,直线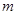 ,
,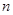 都经过圆C外定点A(1,0).
都经过圆C外定点A(1,0).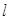 交于N点,且线段PQ的中点为M,
交于N点,且线段PQ的中点为M,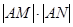 为定值.
为定值.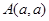 可作圆
可作圆 的两条切线,则实数
的两条切线,则实数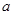 的取值范围为( )
的取值范围为( ) 或
或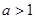
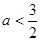
 或
或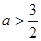
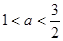
 ,圆C:
,圆C: ,由两圆外一点
,由两圆外一点 引两圆切线PA、PB,切点分别为A、B,满足|PA|=|PB|.
引两圆切线PA、PB,切点分别为A、B,满足|PA|=|PB|.
 上一点,直线l与圆O交于A、B两点,
上一点,直线l与圆O交于A、B两点, ,则
,则 面积的最大值为 .
面积的最大值为 .