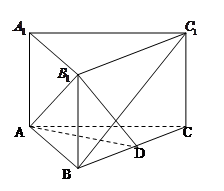题目内容
如图所示,在正三棱柱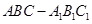 中,底面边长为
中,底面边长为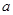 ,侧棱长为
,侧棱长为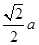 ,
,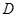 是棱
是棱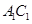 的中点.
的中点.
(Ⅰ)求证: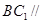 平面
平面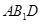 ;(Ⅱ)求二面角
;(Ⅱ)求二面角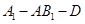 的大小;
的大小;
(Ⅲ)求点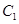 到平面
到平面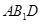 的距离.
的距离.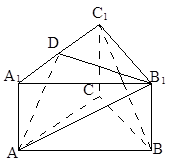
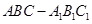 中,底面边长为
中,底面边长为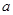 ,侧棱长为
,侧棱长为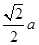 ,
,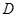 是棱
是棱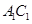 的中点.
的中点.
|
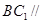 平面
平面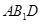 ;(Ⅱ)求二面角
;(Ⅱ)求二面角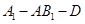 的大小;
的大小;(Ⅲ)求点
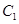 到平面
到平面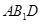 的距离.
的距离.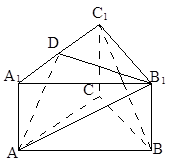
(1)见解析;(2)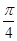 .
.
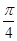 .
.本试题主要考查了立体几何中的线面平行和二面角的求解以及点面距离的求解运算。
证明:(Ⅰ) 连结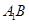 与
与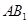 交于
交于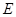 ,
,
则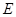 为
为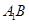 的中点,
的中点,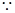
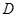 为
为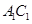 的中点,
的中点,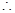
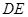 为
为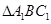 的中位线,
的中位线,
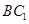 //
//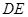 . 又
. 又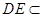 平面
平面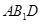 ,
,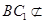 平面
平面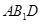
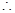
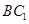 //平面
//平面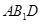
(Ⅱ)(解法1)过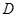 作
作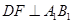 于
于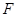 ,由正三棱柱的性质可知,
,由正三棱柱的性质可知,
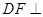 平面
平面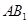 ,连结
,连结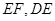 ,在正
,在正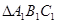 中,
中, 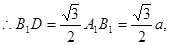
在直角三角形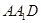 中,
中,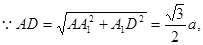
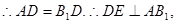
由三垂线定理的逆定理可得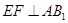 .则
.则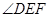 为二面角
为二面角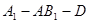 的平面角,
的平面角,
又得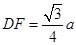 ,
,
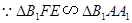 ,
,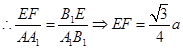
∴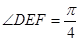 .故所求二面角
.故所求二面角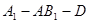 的大小为
的大小为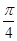 .
.
证明:(Ⅰ) 连结
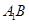 与
与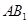 交于
交于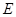 ,
,则
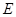 为
为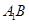 的中点,
的中点,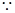
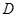 为
为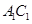 的中点,
的中点,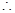
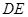 为
为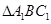 的中位线,
的中位线,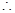
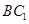 //
//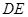 . 又
. 又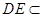 平面
平面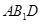 ,
,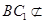 平面
平面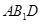
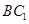 //平面
//平面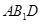
(Ⅱ)(解法1)过
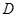 作
作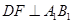 于
于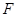 ,由正三棱柱的性质可知,
,由正三棱柱的性质可知,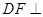 平面
平面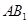 ,连结
,连结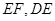 ,在正
,在正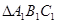 中,
中, 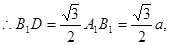
在直角三角形
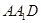 中,
中,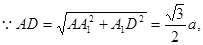
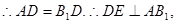
由三垂线定理的逆定理可得
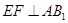 .则
.则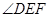 为二面角
为二面角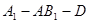 的平面角,
的平面角,又得
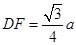 ,
,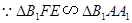 ,
,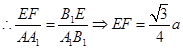
∴
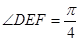 .故所求二面角
.故所求二面角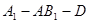 的大小为
的大小为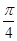 .
.
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
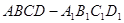 中.
中.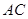 与
与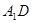 所成角的大小;
所成角的大小;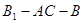 的正切值.
的正切值.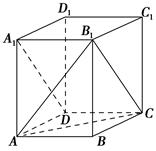
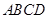 ,
,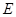 是
是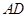 中点,则直线
中点,则直线 与直线
与直线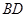 所成的角的余弦值为( )
所成的角的余弦值为( ) 



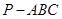 中,
中,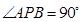 ,
,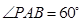 ,
,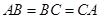 ,平面
,平面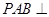 平面
平面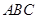 。
。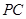 与平面
与平面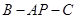 的大小。
的大小。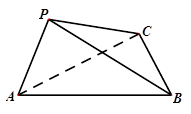
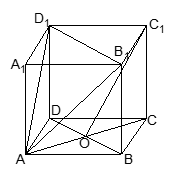
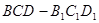 与四棱锥
与四棱锥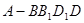 的组合体中,已知
的组合体中,已知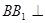 平面
平面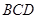 ,四边形
,四边形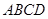 是平行四边形,
是平行四边形,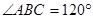 ,
,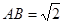 ,
,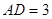 ,
,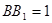 。
。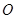 是线段
是线段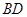 的中点,求证:
的中点,求证: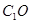 ∥平面
∥平面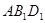 ;
;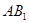 与平面
与平面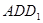 所成的角。
所成的角。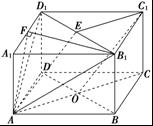
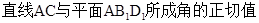 .
.
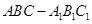 中,
中, 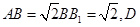 为
为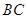 的中点。
的中点。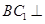 平面
平面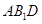 ;(Ⅱ)求直线
;(Ⅱ)求直线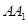 与平面
与平面