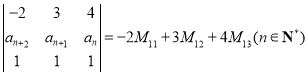题目内容
【题目】已知椭圆![]() 的左.右焦点分别为
的左.右焦点分别为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)若斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,若线段
,若线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的值;
的值;
(2)已知点![]() 是椭圆
是椭圆![]() 上异于椭圆顶点的一点,延长直线
上异于椭圆顶点的一点,延长直线![]() ,
,![]() 分别与椭圆交于点
分别与椭圆交于点![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)设出A,B点坐标,代入椭圆方程作差并整理,则可求出![]() 的值.
的值.
(2)设![]() (
(![]() ),
),![]() ,先计算有一条直线斜率不存在对应的斜率之积的值,再讨论一般情况,求出B,D坐标,化简斜率得出结论.
,先计算有一条直线斜率不存在对应的斜率之积的值,再讨论一般情况,求出B,D坐标,化简斜率得出结论.
(1)设![]() ,将
,将![]() ,
,![]() 作差可得
作差可得
![]() ,
,![]() ,
,![]() ,
,
所以![]() ;
;
(2)设![]() (
(![]() ),
),![]() ,
,
当直线![]() 的斜率不存在时,设
的斜率不存在时,设![]() ,则
,则![]() ,
,
直线![]() 的方程为
的方程为![]() 代入
代入![]() ,可得
,可得![]()
∴![]() ,
,![]() ,则
,则![]() ,
,
∴直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
∴![]() ,当直线
,当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() ,
,![]() 的斜率存在时,
的斜率存在时,![]() ,
,
设直线![]() 的方程为
的方程为![]() ,则由
,则由 消去
消去![]() 可得:
可得:
![]() ,
,
又![]() ,则
,则![]() ,代入上述方程可得
,代入上述方程可得
![]() ,
,
∴![]() ,
,
∴![]() ,则
,则![]()
∴![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,
同理可得![]()
∴直线![]() 的斜率为
的斜率为 ,
,
∵直线![]() 的斜率为
的斜率为![]() ,
,
∴
所以直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() ,即
,即![]() .
.

练习册系列答案
相关题目
【题目】在万众创新的大经济背景下,某成都青年面包店推出一款新面包,每个面包的成本价为![]() 元,售价为
元,售价为![]() 元,该款面包当天只出一炉(一炉至少
元,该款面包当天只出一炉(一炉至少![]() 个,至多
个,至多![]() 个),当天如果没有售完,剩余的面包以每个
个),当天如果没有售完,剩余的面包以每个![]() 元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近
元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近![]() 天的日需求量(单位:个),整理得下表:
天的日需求量(单位:个),整理得下表:
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以![]() 天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为
天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为![]() ,记当日这款新面包获得的总利润为
,记当日这款新面包获得的总利润为![]() (单位:元).求
(单位:元).求![]() 的分布列及其数学期望.
的分布列及其数学期望.
相关公式: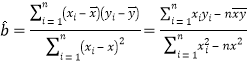 ,
,![]()