题目内容
以直角坐标系的原点为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线l的极坐标方程为 ,圆C的参数方程为
,圆C的参数方程为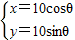 ,(θ为参数),求直线l被圆C截得的弦长.
,(θ为参数),求直线l被圆C截得的弦长.
【答案】分析:先将直线的极坐标方程化成普通方程,然后将圆的参数方程化为普通方程,利用点到直线的距离公式求出点C到直线的距离,最后用垂径公式求出弦长即可.
解答:解:由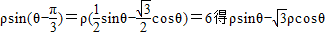 =12.
=12.
∴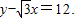
将圆的参数方程化为普通方程为x2+y2=10.圆心为C(0,0),半径为10.
∴点C到直线的距离为
∴直线l被圆截得的弦长为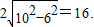
点评:本题主要考查直线和圆的极坐标与参数方程,求弦长,考查运算求解能力及转化的思想,属于基础题.
解答:解:由
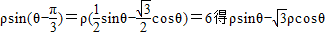 =12.
=12.∴
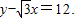
将圆的参数方程化为普通方程为x2+y2=10.圆心为C(0,0),半径为10.
∴点C到直线的距离为

∴直线l被圆截得的弦长为
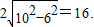
点评:本题主要考查直线和圆的极坐标与参数方程,求弦长,考查运算求解能力及转化的思想,属于基础题.

练习册系列答案
相关题目