题目内容
(注意:本小题为选做题,A,B两题选做其中一题,若都做了,则按A题答案给分)
A.当x,y满足条件|x-1|+|y+1|<1时,变量u=
的取值范围是
B.以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为θ=
(ρ∈R),它与曲线
(α为参数)相交于A,B两点,则以线段AB为直径的圆的面积为
.
A.当x,y满足条件|x-1|+|y+1|<1时,变量u=
| x-1 |
| y-2 |
-
<u<
| 1 |
| 3 |
| 1 |
| 3 |
-
<u<
.| 1 |
| 3 |
| 1 |
| 3 |
B.以直角坐标系的原点为极点,x轴的正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线的极坐标方程为θ=
| π |
| 4 |
|
| 7π |
| 2 |
| 7π |
| 2 |
分析:A、画出|x-1|+|y+1|<1表示的平面区域,借助
的几何意义求解即可.
B、把直线的极坐标方程为θ=
(ρ∈R),曲线
化为直角坐标方程,求出圆的圆心坐标,利用圆心到直线的距离.半径求出半弦长,即可求解以线段AB为直径的圆的面积.
| x-1 |
| y-2 |
B、把直线的极坐标方程为θ=
| π |
| 4 |
|
解答:解:A.|x-1|+|y+1|<1表示的平面区域
变量u=
,表示点M(1,2)与点P两点连线的斜率的倒数.
所以当点P(0,-1)时,
>
⇒
>3
或 当点P(2,-1)时,
<
⇒
<-3,
解得 -
<u<
.
故答案为:-
<u<
.
B.直线的极坐标方程为θ=
(ρ∈R)直角坐标方程为:y=x,
曲线
的直角坐标方程,(x-1)2+(y-2)2=4它的圆心坐标(1,2),半径为2,
圆心到直线的距离d=
=
.半弦长为:
=
,
以线段AB为直径的圆的面积为:πr2=π(
)2=
π.
故答案为:
π.

变量u=
| x-1 |
| y-2 |
所以当点P(0,-1)时,
| 1 |
| u |
| 2-(-1) |
| 1-0 |
| 1 |
| u |
或 当点P(2,-1)时,
| 1 |
| u |
| 2-(-1) |
| 1-2 |
| 1 |
| u |
解得 -
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
| 1 |
| 3 |
B.直线的极坐标方程为θ=
| π |
| 4 |
曲线
|
圆心到直线的距离d=
| |1-2| | ||
|
| 1 | ||
|
22-(
|
|
以线段AB为直径的圆的面积为:πr2=π(
|
| 7 |
| 2 |
故答案为:
| 7 |
| 2 |
点评:本题考查绝对值不等式表示的区域,表达式的几何意义,曲线的参数方程,极坐标方程的应用,考查计算能力,转化思想,作图能力.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
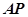 是⊙
是⊙ 的切线,
的切线,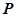 为切点,
为切点,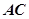 是⊙
是⊙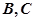 两点,圆心
两点,圆心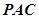 的内部,点
的内部,点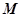 是
是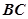 的中点。
的中点。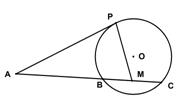
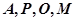 四点共圆;
四点共圆; 的大小。
的大小。 经过点
经过点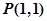 ,倾斜角
,倾斜角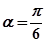 。
。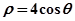 相交于两点
相交于两点 ,求点
,求点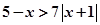 与不等式
与不等式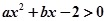 同解,而
同解,而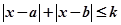 的解集为空集,求实数
的解集为空集,求实数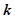 的取值范围。
的取值范围。 的取值范围是 .
的取值范围是 . (ρ∈R),它与曲线
(ρ∈R),它与曲线 (α为参数)相交于A,B两点,则以线段AB为直径的圆的面积为 .
(α为参数)相交于A,B两点,则以线段AB为直径的圆的面积为 .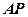 是⊙
是⊙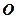 的切线,
的切线,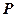 为切点,
为切点,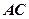 是⊙
是⊙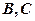 两点,圆心
两点,圆心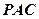 的内部,点
的内部,点
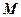 是
是 的中点。
的中点。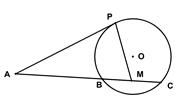
 四点共圆;
四点共圆;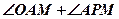 的大小。
的大小。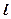 经过点
经过点 ,倾斜角
,倾斜角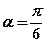 。
。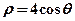 相交于两点
相交于两点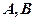 ,求点
,求点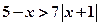 与不等式
与不等式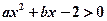 同解,而
同解,而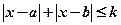 的解集为空集,求实数
的解集为空集,求实数 的取值范围。
的取值范围。