题目内容
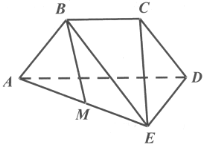
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)详见解析;(2)![]()
【解析】
![]() 利用
利用![]() 与
与![]() 交于
交于![]() ,连接
,连接![]() .证明
.证明![]() ,通过直线与平面平行的判定定理证明
,通过直线与平面平行的判定定理证明![]() 平面
平面![]() ;
;
![]() 对于存在性问题,可先假设存在,即假设
对于存在性问题,可先假设存在,即假设![]() 在线段
在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() .再通过建立空间直角坐标系,求出相关点的坐标,利用坐标法进行求解判断.
.再通过建立空间直角坐标系,求出相关点的坐标,利用坐标法进行求解判断.
![]() 与
与![]() 交于
交于![]() ,连接
,连接![]() .
.
由已知可得四边形![]() 是平行四边形,
是平行四边形,
所以![]() 是
是![]() 的中点.
的中点.
因为![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
![]() 由于四边形
由于四边形![]() 是菱形,
是菱形,![]() ,
,![]() 是
是![]() 的中点,可得
的中点,可得![]() .
.
又四边形![]() 是矩形,面
是矩形,面![]() 面
面![]() ,
,
![]() 面
面![]() ,
,
如图建立空间直角坐标系![]() ,
,
则![]() ,0,
,0,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,2,
,2,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() .
.
则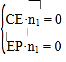 ,
,![]()
![]() ,
,
令![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,
又平面![]() 的法向量
的法向量![]() ,0,
,0,![]() ,
,
![]() ,
,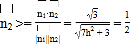 ,解得
,解得![]() ,
,
![]()
![]() ,
,
![]() 在线段
在线段![]() 上不存在点
上不存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
相关题目
【题目】在一次体育兴趣小组的聚会中,要安排6人的座位,使他们在如图所示的6个椅子中就坐,且相邻座位(如1与2,2与3)上的人要有共同的体育兴趣爱好.现已知这6人的体育兴趣爱好如下表所示,且小林坐在1号位置上,则4号位置上坐的是
小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |

A.小方B.小张C.小周D.小马