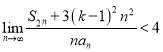题目内容
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() 为常数)
为常数)![]() .
.
(1)求![]() 的值;
的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)记集合![]() ,若
,若![]() 中仅有3个元素,求实数
中仅有3个元素,求实数![]() 的取值范围.
的取值范围.
【答案】(1)  (2)
(2) 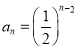 (
(![]() ). (3)
). (3) ![]()
【解析】
(1)由题意列关于![]() ,
,![]() 的方程组,求解方程组得
的方程组,求解方程组得![]() ,
,![]() 的值(2)把(1)中所求
的值(2)把(1)中所求![]() ,
,![]() 值代入
值代入![]() ,取
,取![]() 得另一递推式,作差后可得数列
得另一递推式,作差后可得数列![]() 是等比数列,进一步得到通项公式(3)求出数列
是等比数列,进一步得到通项公式(3)求出数列![]() 的前
的前![]() 项和,代入
项和,代入![]() ,构造函数
,构造函数![]() ,利用作差法判断函数单调性,由单调性求得实数
,利用作差法判断函数单调性,由单调性求得实数![]() 的取值范围.
的取值范围.
(1)由题意,得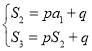 ,
,
即![]() ,解得
,解得 .
.
(2)由(1)知,![]() ①
①
当![]() 时,
时,![]() ②
②
①-②,得![]() (
(![]() ),又
),又![]() ,
,
所以数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
所以![]() 的通项公式为
的通项公式为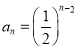 (
(![]() ).
).
(3)由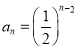 ,得
,得![]() ,
,
得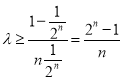 ,令
,令![]() ,
,
因为![]() ,所以
,所以![]() 为递增数列,
为递增数列,
且![]() ,所以
,所以![]() 即可
即可
即 ![]() .
.

练习册系列答案
相关题目