题目内容
已知函数
，
为实数.
（1）当
时，判断函数
的奇偶性，并说明理由；
（2）当
时，指出函数的单调区间（不要过程）；
（3）是否存在实数
，使得在闭区间
上的最大值为2.若存在，求出的值；若不存在，请说明理由
【答案】
（1）
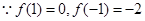
既不是奇函数，又不是偶函数. ……………………………………4分
（2）（画图）
时，
，单调增区间为
时，
，
单调增区间为
，单调减区间为
………………………………8分
（3）
由（2）知，
在
上递增
必在区间
上取最大值2 ……………………………………10分
当
，即
时，
则
，
，成立 ……………………………………12分
当
，即
时，
则
，则
（舍）
综上，
【解析】略
练习册系列答案
教材全解字词句篇系列答案
相关题目
(
，
为实数，且
)，
时，函数
的最小值是
。
在区间
上的值域也为
，求
和
的值。
（
为实数）.
时，
求
的最小值；
上是单调函数，求
（
为实数）.
时，
求
的最小值；
上是单调函数，求
（
为实数，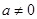
，
）．
的图像过点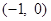
，且方程
有且只有一个根，求
当
，
，
，且函数
能否大于
？
（
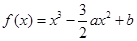为实数，且
），在区间
上最大值为
，最小值为
的解析式
在区间
上为减函数，求实数
的取值范围
作函数
图象的切线，求切线方程