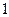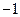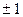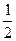题目内容
各项为正数的等比数列{an},a4•a7=8,则log2a1+log2a2+…+log2a10=( )
| A.5 | B.10 | C.15 | D.20 |
由各项为正数的等比数列{an},a4•a7=8,
∴a1a10=a2a9=…=a4a7=…=8.
∴log2a1+log2a2+…+log2a10=log2(a1a2•…•a10)=log285=15.
故答案为:15.
∴a1a10=a2a9=…=a4a7=…=8.
∴log2a1+log2a2+…+log2a10=log2(a1a2•…•a10)=log285=15.
故答案为:15.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
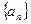 中,
中,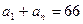 ,
,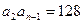 ,前
,前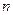 项和
项和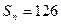 ,求项数
,求项数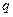 的值。
的值。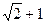 与
与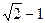 ,两数的等比中项是( )
,两数的等比中项是( )