题目内容
在等比数列{an}中,a4+a7=2,a5a6=-8,则a1+a10=______.
∵在等比数列{an}中,a4+a7=2,a5a6=-8,∴a4+a7=2,且a4•a7=-8.
故a4 和a7是方程x2-x-8=0的两个根,解得a4=4,a7=-2; 或者 a4=-2,a7=4.
若 a4=4,a7=-2,则q3=-
,a1=
=-8,a10=a7•q3=1,∴a1+a10=-7.
若 a4=-2,a7=4,则 q3=-2,a1=
=1,a10=a7•q3=-8,∴a1+a10=-7.
综上可得,a1+a10=-7,
故答案为-7.
故a4 和a7是方程x2-x-8=0的两个根,解得a4=4,a7=-2; 或者 a4=-2,a7=4.
若 a4=4,a7=-2,则q3=-
| 1 |
| 2 |
| a4 |
| q3 |
若 a4=-2,a7=4,则 q3=-2,a1=
| a4 |
| q3 |
综上可得,a1+a10=-7,
故答案为-7.

练习册系列答案
相关题目
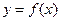 是一次函数,若
是一次函数,若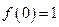 且
且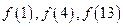 成
成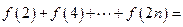 ;
;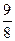 ,末项为
,末项为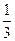 ,公比为
,公比为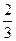 ,则项数
,则项数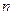 等于 .
等于 .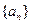 的公比
的公比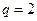 ,前n项和为
,前n项和为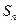 ,则
,则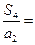 ( )
( )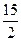
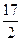
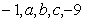 成等比数列,那么( )
成等比数列,那么( )



