题目内容
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC, 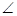 ABC=
ABC=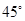 ,AB=2
,AB=2 ,BC=2AE=4,
,BC=2AE=4,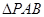 是等腰三角形.
是等腰三角形.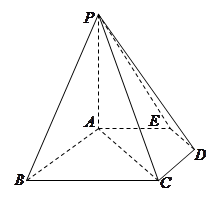
(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)求四棱锥P—ACDE的体积.
(Ⅰ)先证 (Ⅱ)
(Ⅱ)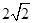
解析试题分析:(Ⅰ)证明:因为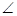 ABC=45°,AB=2
ABC=45°,AB=2 ,BC=4,所以在
,BC=4,所以在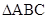 中,由余弦定理得:
中,由余弦定理得: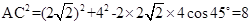 ,解得
,解得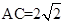 ,
,
所以 ,即
,即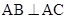 ,又PA⊥平面ABCDE,所以PA⊥
,又PA⊥平面ABCDE,所以PA⊥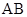 ,
,
又PA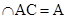 ,所以
,所以 ,又AB∥CD,所以
,又AB∥CD,所以 ,又因为
,又因为 ,所以平面PCD⊥平面PAC;
,所以平面PCD⊥平面PAC;
(Ⅱ)由(Ⅰ)知 ,所以
,所以 ,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得
,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得 ,AC=
,AC=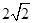 ,所以四边形ACDE的面积为
,所以四边形ACDE的面积为 ,所以四棱锥P—ACDE的体积为
,所以四棱锥P—ACDE的体积为 =
=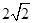 .
.
考点:平面与平面垂直的判定;体积;空间中直线与平面之间的位置关系;直线与平面所成的角.
点评:本题主要考查空间中的基本关系,考查线面垂直、面面垂直的判定以及线面角和几何体体积的计算,考查识图能力、空间想象能力和逻辑推理能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
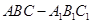 中,
中,  ,
, ,
, ,点
,点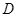 是
是 的中点,
的中点,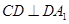 .
.
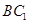 ∥平面
∥平面 ;
; 在线段
在线段 上,
上,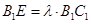 ,且使直线
,且使直线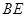 和平面
和平面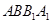 所成的角的正弦值为
所成的角的正弦值为 ,求
,求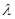 的值.
的值. 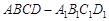 中,侧棱
中,侧棱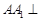 底面
底面 ,
,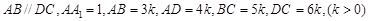
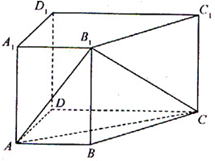
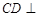 平面
平面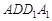
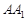 与平面
与平面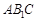 所成角的正弦值为
所成角的正弦值为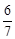 ,求
,求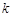 的值
的值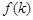 ,写出
,写出 中,
中,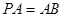 ,点M,N分别在PA,BD上,且
,点M,N分别在PA,BD上,且 .
.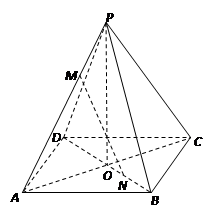
 ∥平面PBC;
∥平面PBC;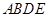 ⊥平面
⊥平面 ,
, ,
,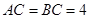 ,四边形
,四边形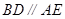 ,
,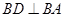 ,
,  ,
, 分别为
分别为 的中点.
的中点. 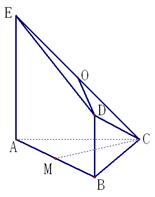
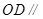 平面
平面 平面
平面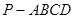 中,底面
中,底面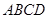 是正方形,
是正方形, 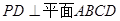 ,
,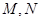 分别为
分别为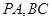 的中点,且
的中点,且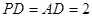 .
.
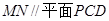 ;
;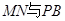 所成的角的余弦值
所成的角的余弦值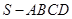 的底面
的底面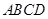 是直角梯形,
是直角梯形,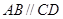 ,
,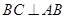 ,侧面
,侧面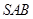 为正三角形,
为正三角形,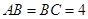 ,
,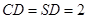 .如图所示.
.如图所示.
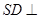 平面
平面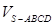 .
. 的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=
的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=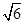 ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点.
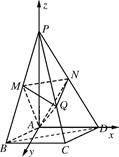
 的底面是正方形,
的底面是正方形, ,点
,点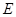 在棱
在棱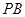 上.
上.
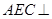 平面
平面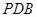 ;
;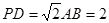 ,且
,且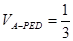 时,确定点
时,确定点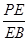 的值.
的值.