题目内容
如图,在四棱锥P-ABCD中,底面是边长为2 的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=
的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=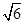 ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点.
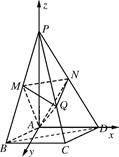
(1)证明:MN∥平面ABCD;
(2) 过点A作AQ⊥PC,垂足为点Q,求二面角A-MN-Q的平面角的余弦值.
(1)只需证 MN∥BD;(2)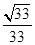 。
。
解析试题分析:(1)如图,连接BD.∵M,N分别为PB,PD的中点,∴在△PBD中,MN∥BD.
又MN?平面ABCD,∴MN∥平面ABCD.
(2)如图建系:A(0,0,0),P(0,0,2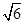 ),M
),M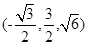 ,N(
,N( ,0,
,0,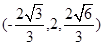 ),C(
),C( ,3,0).
,3,0).
设Q(x,y,z),则C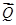 =(x-
=(x- ,y-3,z),C
,y-3,z),C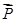 =(-
=(- ,-3,2
,-3,2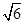 ).
).
∵C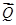 =λC
=λC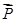 =(-
=(- λ,-3λ,2
λ,-3λ,2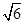 λ),∴Q(
λ),∴Q( -
- λ,3-3λ,2
λ,3-3λ,2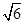 λ).
λ).
由A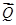 ⊥C
⊥C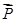 ⇒A
⇒A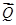 ·C
·C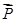 =0,得λ=
=0,得λ=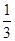 .即:Q
.即:Q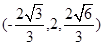
对于平面AMN:设其法向量为n=(a,b,c).
∵A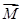 =
= ,A
,A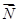 =(
=( ,0,
,0,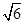 ).
).
则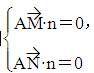 ⇒
⇒ ⇒
⇒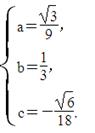
∴n=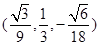 .
.
同理对于平面QMN,得其法向量为v=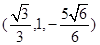
记所求二面角A-MN-Q的平面角大小为θ,则cosθ=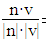
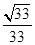 .
.
∴所求二面角A-MN-Q的平面角的余弦值为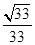 .
.
考点:线面垂直的性质定理;线面平行的判定定理;二面角。
点评:二面角的求法是立体几何中的一个难点。我们解决此类问题常用的方法有两种:①综合法,综合法的一般步骤是:一作二说三求。②向量法,运用向量法求二面角应注意的是计算。很多同学都会应用向量法求二面角,但结果往往求不对,出现的问题就是计算错误。

练习册系列答案
相关题目
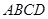 中,
中,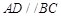 ,
,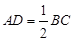 ,
,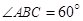 ,
, 是
是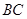 的中点.将梯形
的中点.将梯形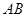 旋转
旋转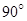 ,得到梯形
,得到梯形 (如图).
(如图).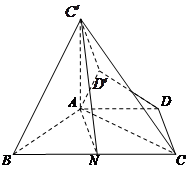
 平面
平面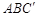 ;
; 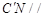 平面
平面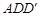 ;
;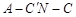 的余弦值.
的余弦值.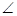 ABC=
ABC=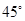 ,AB=2
,AB=2 ,BC=2AE=4,
,BC=2AE=4,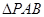 是等腰三角形.
是等腰三角形.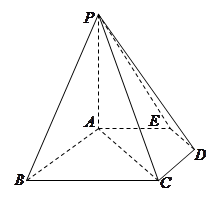
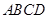 中,
中,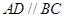 ,
,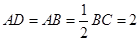 ,
,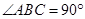 ,
,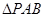 是等边三角形,平面
是等边三角形,平面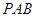 ⊥平面
⊥平面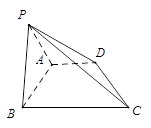
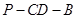 的余弦值;
的余弦值;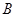 到平面
到平面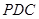 的距离.
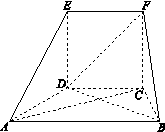
的距离.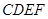 为正方形,面
为正方形,面 为等腰梯形,
为等腰梯形,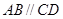 ,
,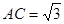 ,
,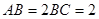 ,
,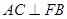 .
.
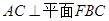 ;
;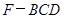 的体积;
的体积; 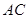 上是否存在点
上是否存在点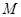 ,使
,使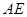 //平面
//平面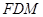 ?证明你的结论.
?证明你的结论.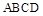 与
与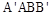 都是边长为
都是边长为 的正方形,点E是
的正方形,点E是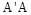 的中点,
的中点,
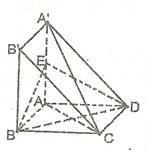
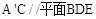 ;
;  ;
;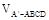 与
与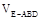 的比值。
的比值。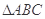 是等腰直角三角形,其中
是等腰直角三角形,其中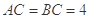 ,
,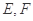 分别为
分别为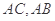 的中点,将
的中点,将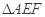 沿
沿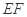 折起,点
折起,点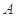 的位置变为点
的位置变为点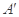 ,已知点
,已知点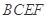 上的射影
上的射影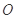 为
为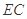 的中点,如图(2)所示.
的中点,如图(2)所示.
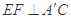 ;
;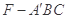 的体积.
的体积.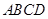 中,
中,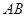 ,
,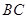 ,
,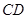 两两互相垂直,且
两两互相垂直,且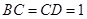 .
.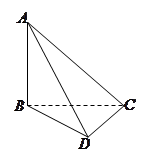
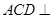 平面
平面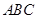 ;
;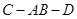 的大小;
的大小; 与平面
与平面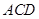 所成的角为
所成的角为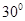 ,求线段
,求线段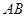 为圆
为圆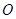 的直径,点
的直径,点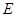 、
、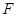 在圆
在圆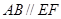 ,矩形
,矩形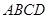 所在的平面与圆
所在的平面与圆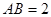 ,
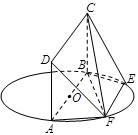
,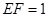 .
.
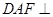 平面
平面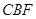 ;
;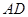 的长为何值时,平面
的长为何值时,平面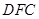 与平面
与平面 所成的锐二面角的大小为
所成的锐二面角的大小为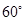 ?
?