题目内容
若函数 在
在 上为增函数,则实数
上为增函数,则实数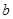 的取值范围为( )
的取值范围为( )
A.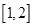 | B.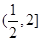 | C.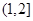 | D.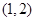 |
A
解析试题分析:f1(x)=(2b-1)x+b-1(x>0),f2(x)=-x2+(2-b)x(x≤0),要使f(x)在R上为增函数,须有f1(x)递增,f2(x)递增,且f2(0)≤f1(0),即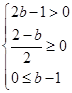 ,解得1≤b≤2.故选A.
,解得1≤b≤2.故选A.
考点:本题考查了分段函数的单调性
点评:考查函数单调性的性质,应熟练数掌握形结合思想在分析问题中的应用

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
函数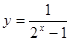 的值域是 ( )
的值域是 ( )
A.(-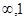 ) ) | B.(-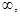 0) 0)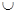 (0,+ (0,+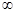 ) ) |
C.(-1,+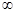 ) ) | D.(-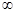 ,-1) ,-1)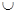 (0,+ (0,+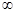 ) ) |
已知方程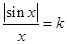 在
在 有两个不同的解
有两个不同的解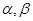 (
(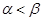 ),则下面结论正确的是:
),则下面结论正确的是:
A.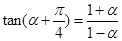 | B.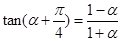 |
C.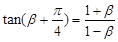 | D.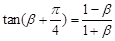 |
已知函数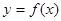 的图象如图①所示,则图②是下列哪个函数的图象 c
的图象如图①所示,则图②是下列哪个函数的图象 c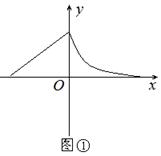

A.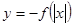 | B.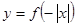 | C.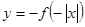 | D.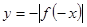 |
若函数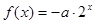 与
与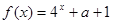 的图象有交点,则
的图象有交点,则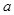 的取值范围是( )
的取值范围是( )
A.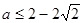 或 或 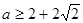 |
B.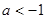 |
C.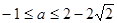 |
D.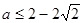 |
若函数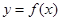 的定义域为
的定义域为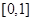 , 则下列函数中可能是偶函数的是 ( ).
, 则下列函数中可能是偶函数的是 ( ).
A.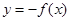 | B.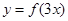 | C.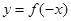 | D.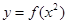 |
下列函数中既是偶函数,又在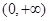 单调递增的函数是( ) .
单调递增的函数是( ) .
A. | B. | C.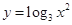 | D.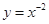 |
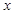
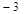
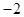
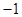
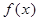
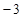
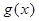
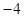
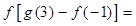 ( )
( )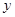 轴相交。②奇函数的图像不一定过原点。③偶函数若在
轴相交。②奇函数的图像不一定过原点。③偶函数若在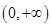 上是减函数,则在
上是减函数,则在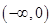 上一定是增函数。④有且只有一个函数既是奇函数又是偶函数。其中正确结论的个数是( )
上一定是增函数。④有且只有一个函数既是奇函数又是偶函数。其中正确结论的个数是( )