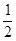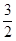题目内容
已知方程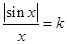 在
在 有两个不同的解
有两个不同的解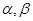 (
(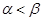 ),则下面结论正确的是:
),则下面结论正确的是:
A.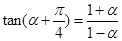 | B.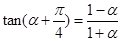 |
C.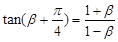 | D.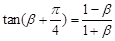 |
C
解析试题分析: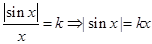 ,要使方程
,要使方程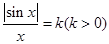 在
在 有两个不同的解,则
有两个不同的解,则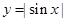 的图像与直线
的图像与直线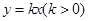 有且仅有三个公共点,所以直线
有且仅有三个公共点,所以直线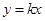 与
与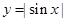 在
在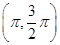 内相切,且切于点
内相切,且切于点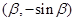 ,由
,由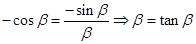 ,
,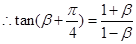 .
.
考点:本小题主要考查三角函数的图象,函数的零点,三角函数的计算.
点评:解决本小题的关键是将方程有两个不同的解转化成两个函数图象有且仅有三个公共点,进而求出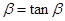 ,考查学生对问题的转化能力.
,考查学生对问题的转化能力.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
函数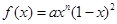 在区间〔0,1〕上的图像如图所示,则n可能是( )
在区间〔0,1〕上的图像如图所示,则n可能是( )
| A.1 | B.2 | C.3 | D.4 |
已知函数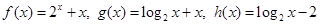 的零点依次为
的零点依次为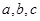 ,则( )
,则( )
A.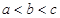 | B.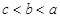 | C.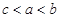 | D.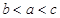 |
函数 的零点所在的大致区间是 ( )
的零点所在的大致区间是 ( )
A.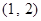 | B.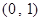 | C.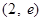 | D.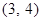 |
若函数 在
在 上为增函数,则实数
上为增函数,则实数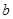 的取值范围为( )
的取值范围为( )
A.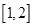 | B.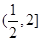 | C.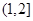 | D.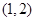 |
函数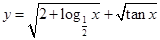 的定义域是( )
的定义域是( )
A. | B.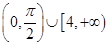 |
C.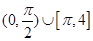 | D.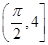 |
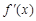 的图象如右图所示,那么函数f (x)的图象最有可能的是
的图象如右图所示,那么函数f (x)的图象最有可能的是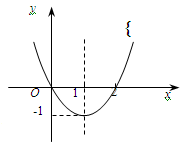
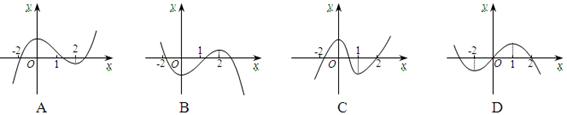
 在定义域内可导,
在定义域内可导,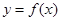 的图象如下左图所示,则导函数
的图象如下左图所示,则导函数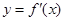 的图象可能是
的图象可能是
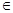 R)为奇函数, f(2)="1," f(x+2)=f(x)+f(2),则f(3)等于( )
R)为奇函数, f(2)="1," f(x+2)=f(x)+f(2),则f(3)等于( )