题目内容
下列函数中既是偶函数,又在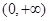 单调递增的函数是( ) .
单调递增的函数是( ) .
A. | B. | C.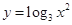 | D.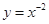 |
C
解析试题分析:对于选项A,由于函数 ,是过原点的奇函数,因此不符合题意,
,是过原点的奇函数,因此不符合题意,
对于选项B,由于 是偶函数 ,但是在
是偶函数 ,但是在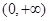 是单调递减的,因此错误
是单调递减的,因此错误
对于C,由于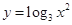 ,是复合函数,是偶函数,同时内外结合可知在第一象限是减函数,故成立,
,是复合函数,是偶函数,同时内外结合可知在第一象限是减函数,故成立,
对于选项D,由于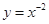 是偶函数,但是由于在
是偶函数,但是由于在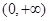 是单调递减的,因此错误
是单调递减的,因此错误
故选C.
考点:函数的性质运用
点评:解决该试题的关键是对于常见函数性质的熟练掌握,属于基础题。

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
若函数 在
在 上为增函数,则实数
上为增函数,则实数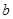 的取值范围为( )
的取值范围为( )
A.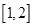 | B.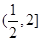 | C.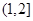 | D.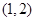 |
已知函数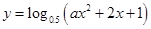 的定义域是
的定义域是 ,则实数
,则实数 取值范围是( )
取值范围是( )
A.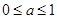 | B.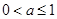 | C.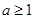 | D.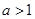 |
函数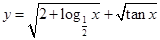 的定义域是( )
的定义域是( )
A. | B.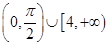 |
C.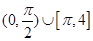 | D.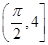 |
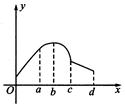
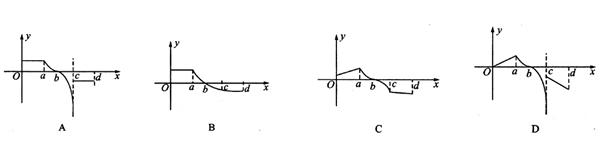
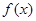 在定义域内可导,
在定义域内可导,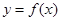 的图象如下左图所示,则导函数
的图象如下左图所示,则导函数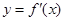 的图象可能是
的图象可能是
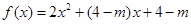 ,
,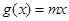 ,若对于任一实数
,若对于任一实数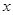 ,
,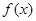 与
与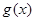 的值至少有一个为正数,则实数
的值至少有一个为正数,则实数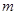 的取值范围是( )
的取值范围是( )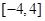
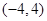
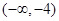

 与
与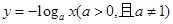 在同一坐标系中的图像只可能是 ( )
在同一坐标系中的图像只可能是 ( )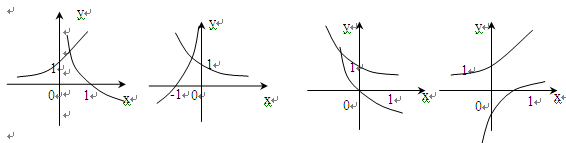
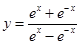 的图像大致为( ).
的图像大致为( ).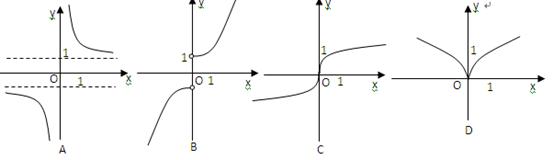
 的图象如图所示,则
的图象如图所示,则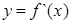 的大致图象可以是图中的( )
的大致图象可以是图中的( )