题目内容
(2012•济南三模)下列正确命题的序号是
(1)“m=-2”是直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直的必要不充分条件;
(2)?a∈R,使得函数y=|x+1|+|x+a|是偶函数;
(3)不等式:
•1≥
•
,
•(1+
)≥
•(
+
),
•(1+
+
)≥
•(
+
+
),…,由此猜测第n个不等式为
(1+
+
+…+
)≥
•(
+
+
)…+
)
(4)若二项式(x+
)n的展开式中所有项的系数之和为243,则展开式中x-4的系数是40.
(2)(3)
(2)(3)
(1)“m=-2”是直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直的必要不充分条件;
(2)?a∈R,使得函数y=|x+1|+|x+a|是偶函数;
(3)不等式:
| 1 |
| 2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| n+1 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2n |
(4)若二项式(x+
| 2 |
| x2 |
分析:(1)直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直时,(m+2)(m-2)+m(m+2)=0,可得m=-2或m=1;(2)当a=-1时,y=|x+1|+|x-1|为偶函数;由归纳推理可知,(3)正确;(4)先求展开式的通项,再求展开式中x-4的系数即可.
解答:解:当m=-2时,两直线为y=
和x=-
,此时两直线垂直,反之,直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直时,(m+2)(m-2)+m(m+2)=0,∴m=-2或m=1,∴“m=-2”是直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直的充分不必要条件,所以(1)错误;
所以当a=-1时,y=|x+1|+|x-1|为偶函数,所以(2)正确;
由归纳推理可知,(3)正确;
令x=1,则得所有项系数为3n=243,解得n=5,二项式的通项公式为Tk+1=
x5-k(
)k=
x5-3k2k,
令5-3k=-4,得k=3,所以T4=
x-423,所以系数为
23=80,所以(4)错误,
故正确的为(2)(3).
故答案为:(2)(3)
| 1 |
| 2 |
| 3 |
| 4 |
所以当a=-1时,y=|x+1|+|x-1|为偶函数,所以(2)正确;
由归纳推理可知,(3)正确;
令x=1,则得所有项系数为3n=243,解得n=5,二项式的通项公式为Tk+1=
| C | k 5 |
| 2 |
| x2 |
| C | k 5 |
令5-3k=-4,得k=3,所以T4=
| C | 3 5 |
| C | 3 5 |
故正确的为(2)(3).
故答案为:(2)(3)
点评:本题考查命题真假判断,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
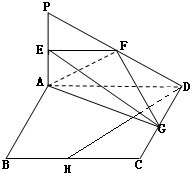 (2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.
(2012•济南三模)如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且2PA=AD,E、F、G、H分别是线段PA、PD、CD、BC的中点.