题目内容
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:
(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅲ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记ξ表示抽到“好视力”学生的人数,求ξ的分布列及数学期望.
分析:(1)根据所给的茎叶图看出16个数据,找出众数和中位数,中位数需要按照从小到大的顺序排列得到结论.
(2)由题意知本题是一个古典概型,至多有1人是“好视力”包括有一个人是好视力和有零个人是好视力,根据古典概型公式得到结果.
(3)由于从该校任选3人,记ξ表示抽到“好视力”学生的人数,得到变量的可能取值是0、1、2、3,结合变量对应的事件,算出概率,写出分布列和期望.
(2)由题意知本题是一个古典概型,至多有1人是“好视力”包括有一个人是好视力和有零个人是好视力,根据古典概型公式得到结果.
(3)由于从该校任选3人,记ξ表示抽到“好视力”学生的人数,得到变量的可能取值是0、1、2、3,结合变量对应的事件,算出概率,写出分布列和期望.
解答:解:(Ⅰ)∵4.6和4.7都出现三次,
∴众数:4.6和4.7;中位数:4.75
(Ⅱ)由题意知本题是一个古典概型,
设Ai表示所取3人中有i个人是“好视力”,
至多有1人是“好视力”记为事件A,包括有一个人是好视力和有零个人是好视力,
∴P(A)=P(A0)+P(A1)=
+
=
.
(Ⅲ)ξ的可能取值为0、1、2、3
P(ξ=0)=(
)3=
P(ξ=1)=
(
)2=
P(ξ=2)=
(
)2
=
P(ξ=3)=(
)3=
∴分布列为
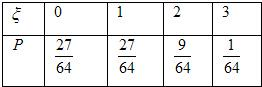
∴Eξ=1×
+2×
+3×
=0.75
∴众数:4.6和4.7;中位数:4.75
(Ⅱ)由题意知本题是一个古典概型,
设Ai表示所取3人中有i个人是“好视力”,
至多有1人是“好视力”记为事件A,包括有一个人是好视力和有零个人是好视力,
∴P(A)=P(A0)+P(A1)=
| ||
|
| ||||
|
| 121 |
| 140 |
(Ⅲ)ξ的可能取值为0、1、2、3
P(ξ=0)=(
| 3 |
| 4 |
| 27 |
| 64 |
| C | 1 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 27 |
| 64 |
| C | 2 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 9 |
| 64 |
| 1 |
| 4 |
| 1 |
| 64 |
∴分布列为

∴Eξ=1×
| 27 |
| 64 |
| 9 |
| 24 |
| 1 |
| 64 |
点评:本题是一个统计综合题,对于一组数据,通常要求的是这组数据的众数,中位数,平均数,题目分别表示一组数据的特征,这样的问题可以出现在选择题或填空题.考查最基本的知识点.

练习册系列答案
相关题目
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图示:
|
|
|
|
4 |
3 5 6 6 6 7 7 7 8 8 9 9 |
|
5 |
0 1 1 2 |
|
|
|
指出这组数据的众数和中位数;
若视力测试结果不低于5.0,则称为“健康视力”,求校医从这16人中随机选取3人,至多有1人是“健康视力”的概率;以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记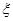 表示抽到“健康视力”学生的人数,求
表示抽到“健康视力”学生的人数,求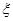 的分布列及数学期望
的分布列及数学期望
 (2014•达州一模)由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检査得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图:
(2014•达州一模)由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检査得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图: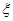 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求
