题目内容
 (2014•达州一模)由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检査得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图:
(2014•达州一模)由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检査得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图:(I )若视力测试结果不低于5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(II)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记ξ表示抽到“好视力”学生的人数,求ξ的分布列及数学期望.
分析:(1)由题意知本题是一个古典概型,至多有1人是“好视力”包括有一个人是好视力和有零个人是好视力,根据古典概型公式得到结果
(2)由于从该校任选3人,记ξ表示抽到“好视力”学生的人数,得到变量的可能取值是0、1、2、3,结合变量对应的事件,算出概率,写出分布列和期望
(2)由于从该校任选3人,记ξ表示抽到“好视力”学生的人数,得到变量的可能取值是0、1、2、3,结合变量对应的事件,算出概率,写出分布列和期望
解答:解:(1)设Ai表示所取的3人中有i个人是“好视力”,设事件A:至多有一个人是“好视力”
则P(A)=P(A0)+P(A1)=
+
=
(2)每个人是“好视力”的概率为
=
ξ的可能取值为0、1、2、3
P(ξ=0)=(1-
)3=
P(ξ=1)=
(1-
)2=
P(ξ=2)=
(
)2(1-
) =
P(ξ=3)=(
)3=
∴ξ的分布列为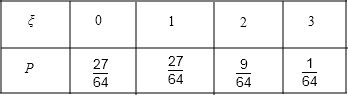
期望为Eξ=0×
+1×
+2×
+3×
=
则P(A)=P(A0)+P(A1)=
| ||
|
| ||||
|
| 121 |
| 140 |
(2)每个人是“好视力”的概率为
| 4 |
| 16 |
| 1 |
| 4 |
ξ的可能取值为0、1、2、3
P(ξ=0)=(1-
| 1 |
| 4 |
| 27 |
| 64 |
| C | 1 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 27 |
| 64 |
P(ξ=2)=
| C | 2 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 9 |
| 64 |
| 1 |
| 4 |
| 1 |
| 64 |
∴ξ的分布列为

期望为Eξ=0×
| 27 |
| 64 |
| 27 |
| 64 |
| 9 |
| 64 |
| 1 |
| 64 |
| 3 |
| 4 |
点评:本题考查茎叶图和离散型随机变量的概率.要求会读敬业图,掌握互斥事件的概率加法公式和n次独立实验的概率求法.确定变量的取值,正确求概率是关键.属简单题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2014•达州一模)已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).
(2014•达州一模)已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).