题目内容
【题目】如图，已知椭圆C： 
+ 
=1（a＞b＞0）的离心率e= 
，过点（0，﹣b），（a，0）的直线与原点的距离为 
，M（x0 ， y0）是椭圆上任一点，从原点O向圆M：（x﹣x0）2+（y﹣y0）2=2作两条切线，分别交椭圆于点P，Q．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若记直线OP，OQ的斜率分别为k1 ， k2 ， 试求k1k2的值．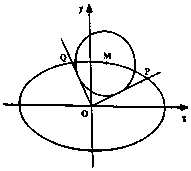
【答案】解：（Ⅰ）由椭圆的离心率e= 
= 
= 
，
即a2=2b2 ， ①
设过点（0，﹣b），（a，0）的直线方程为 
，
即bx﹣ay﹣ab=0，
因为直线与原点的距离为 
，
∴ 
= ，整理得： 
=2，②
由①②得 
，
∴椭圆的方程为 
；
（Ⅱ）由直线OP：y=k1x，OQ：y=k2x，与圆M相切，
由直线和圆相切的条件：d=r，可得 
= 
= ，
平方整理，可得k12（2﹣x02）+2k1x0y0+2﹣y02=0，
k22（2﹣x02）+2k2x0y0+2﹣y02=0，
∴k1 ， k2是方程k2（2﹣x02）+2kx0y0+2﹣y02=0的两个不相等的实数根，
k1k2= 
，
由点R（x0 ， y0）在椭圆C上，
∴ 
，即y02=3（1﹣ 
）=3﹣ 
x02 ，
∴k1k2= 
=﹣ ，
k1k2的值为﹣ ．
【解析】（Ⅰ）由椭圆的离心率公式可知a2=2b2 ， 利用点到直线的距离公式 =2，即可求得a和b的值，即可求得椭圆方程；（Ⅱ）利用点到直线的距离公式，可知k1 ， k2是方程k2（2﹣x02）+2kx0y0+2﹣y02=0的两个不相等的实数根，利用韦达定理即可求得k1k2 ， 由R（x0 ， y0）在椭圆C上，y02=3﹣ x02 ， 代入即可求得k1k2的值．
练习册系列答案
相关题目
