题目内容
【题目】已知函数f(x)=x2+2alnx.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)求函数f(x)的单调区间;
(3)若函数 ![]() 在[1,2]上是减函数,求实数a的取值范围.
在[1,2]上是减函数,求实数a的取值范围.
【答案】
(1)
解: ![]()
由已知f'(2)=1,解得a=﹣3.
(2)
函数f(x)的定义域为(0,+∞).
(i)当a≥0时,f'(x)>0,f(x)的单调递增区间为(0,+∞);
(ii)当a<0时 ![]() .
.
当x变化时,f'(x),f(x)的变化情况如下:
x |
|
|
|
f'(x) | ﹣ | 0 | + |
f(x) | 极小值 |
由上表可知,函数f(x)的单调递减区间是 ![]() ;
;
单调递增区间是 ![]() .
.
(3)
由 ![]() 得
得 ![]() ,
,
由已知函数g(x)为[1,2]上的单调减函数,
则g'(x)≤0在[1,2]上恒成立,
即 ![]() 在[1,2]上恒成立.
在[1,2]上恒成立.
即 ![]() 在[1,2]上恒成立.
在[1,2]上恒成立.
令 ![]() ,在[1,2]上
,在[1,2]上 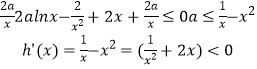 ,
,
所以h(x)在[1,2]为减函数. ![]() ,
,
所以 ![]()
【解析】(Ⅰ)先对函数求导,然后由由已知f'(2)=1,可求a(II)先求函数f(x)的定义域为(0,+∞),要判断函数的单调区间,需要判断导数 ![]() 的正负,分类讨论:分(1)当a≥0时,(2)当a<0时两种情况分别求解(II)由g(x)可求得g′(x),由已知函数g(x)为[1,2]上的单调减函数,可知g'(x)≤0在[1,2]上恒成立,即
的正负,分类讨论:分(1)当a≥0时,(2)当a<0时两种情况分别求解(II)由g(x)可求得g′(x),由已知函数g(x)为[1,2]上的单调减函数,可知g'(x)≤0在[1,2]上恒成立,即 ![]() 在[1,2]上恒成立,要求a的范围,只要求解
在[1,2]上恒成立,要求a的范围,只要求解 ![]() ,在[1,2]上的最小值即可
,在[1,2]上的最小值即可
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目