题目内容
18.设a+b=2,b>0,当$\frac{1}{2|a|}$+$\frac{|a|}{b}$取得最小值时,a=-2.分析 由题意得$\frac{1}{2|a|}$+$\frac{|a|}{b}$=$\frac{1}{2|a|}$+$\frac{|a|}{2-a}$,(a<2);从而构造函数f(a)=$\frac{1}{2|a|}$+$\frac{|a|}{2-a}$,(a<2),从而作函数的图象辅助,当a<0时,f(a)=-$\frac{1}{2a}$+$\frac{a}{a-2}$,f′(a)=$\frac{1}{2{a}^{2}}$-$\frac{2}{(a-2)^{2}}$=$\frac{-(3a-2)(a+2)}{2{a}^{2}(a-2)^{2}}$,从而确定函数的单调性及最值;同理确定当0<a<2时的单调性及最值,从而解得.
解答 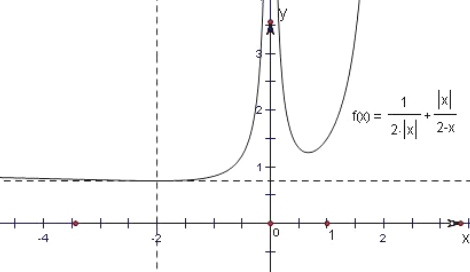 解:∵a+b=2,b>0,
解:∵a+b=2,b>0,
∴$\frac{1}{2|a|}$+$\frac{|a|}{b}$=$\frac{1}{2|a|}$+$\frac{|a|}{2-a}$,(a<2);
设f(a)=$\frac{1}{2|a|}$+$\frac{|a|}{2-a}$,(a<2),
作此函数的图象,如右图所示;
利用导数研究其单调性得,
当a<0时,f(a)=-$\frac{1}{2a}$+$\frac{a}{a-2}$,
f′(a)=$\frac{1}{2{a}^{2}}$-$\frac{2}{(a-2)^{2}}$=$\frac{-(3a-2)(a+2)}{2{a}^{2}(a-2)^{2}}$,
当a<-2时,f′(a)<0,当-2<a<0时,f′(a)>0,
故函数在(-∞,-2)上是减函数,在(-2,0)上是增函数,
∴当a=-2时,$\frac{1}{2|a|}$+$\frac{|a|}{2-a}$取得最小值$\frac{3}{4}$;
同理,当0<a<2时,得到当a=$\frac{3}{4}$时,
$\frac{1}{2|a|}$+$\frac{|a|}{2-a}$取得最小值$\frac{5}{4}$;.
综合,则当a=-2时,$\frac{1}{2|a|}$+$\frac{|a|}{2-a}$取得最小值;
故答案为:-2.
点评 本题考查了导数的综合应用及数形结合的思想应用.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案| A. | [-2,6] | B. | [-3,6] | C. | [-2,4] | D. | [-3,8] |
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
| A. | $\frac{7}{25}$ | B. | $\frac{7}{25}$$\sqrt{2}$ | C. | $\frac{17\sqrt{2}}{50}$ | D. | $\frac{17}{25}$$\sqrt{2}$ |