题目内容
已知椭圆C: =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为 时,求k的值.
时,求k的值.
 =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.(1)求椭圆C的方程;
(2)当△AMN的面积为
 时,求k的值.
时,求k的值.(1) =1(2)k=±1.
=1(2)k=±1.
 =1(2)k=±1.
=1(2)k=±1.(1)由题意得 解得b=
解得b=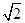 ,所以椭圆C的方程为
,所以椭圆C的方程为 =1.
=1.
(2)由 得(1+2k2)x2-4k2x+2k2-4=0.设点M,N的坐标分别为(x1,y1),(x2,y2),
得(1+2k2)x2-4k2x+2k2-4=0.设点M,N的坐标分别为(x1,y1),(x2,y2),
则y1=k(x1-1),y2=k(x2-1),x1+x2= ,x1x2=
,x1x2= ,
,
所以MN= =
= .
.
又因为点A(2,0)到直线y=k(x-1)的距离d= ,所以△AMN的面积为S=
,所以△AMN的面积为S= MN·d=
MN·d= .由
.由 =
= ,解得k=±1.
,解得k=±1.
 解得b=
解得b=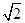 ,所以椭圆C的方程为
,所以椭圆C的方程为 =1.
=1.(2)由
 得(1+2k2)x2-4k2x+2k2-4=0.设点M,N的坐标分别为(x1,y1),(x2,y2),
得(1+2k2)x2-4k2x+2k2-4=0.设点M,N的坐标分别为(x1,y1),(x2,y2),则y1=k(x1-1),y2=k(x2-1),x1+x2=
 ,x1x2=
,x1x2= ,
,所以MN=
 =
= .
.又因为点A(2,0)到直线y=k(x-1)的距离d=
 ,所以△AMN的面积为S=
,所以△AMN的面积为S= MN·d=
MN·d= .由
.由 =
= ,解得k=±1.
,解得k=±1.
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
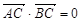 ,|BC|=2|AC|.
,|BC|=2|AC|.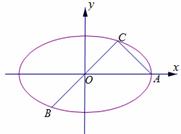
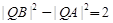 ?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.
?若存在,有几个(不必求出Q点的坐标),若不存在,请说明理由.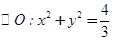 的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明:
的两条切线,切点分别为M、N,若直线MN在x轴、y轴上的截距分别为m、n,证明: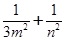 为定值.
为定值.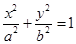 (
(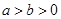 )的短轴长为2,离心率为
)的短轴长为2,离心率为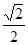 .
.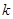 的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足
的直线与椭圆C相交于两点G、H,设P为椭圆C上一点,且满足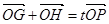 (O为坐标原点),当
(O为坐标原点),当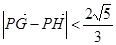 时,求实数
时,求实数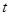 的取值范围?
的取值范围?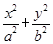 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为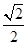 ,短轴的一个端点为M(0,1),直线l:y=kx-
,短轴的一个端点为M(0,1),直线l:y=kx-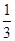 与椭圆相交于不同的两点A、B.
与椭圆相交于不同的两点A、B.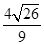 ,求k的值;
,求k的值; =1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
=1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
 ,求实数m;
,求实数m; 的值是否与θ的大小无关,并证明你的结论.
的值是否与θ的大小无关,并证明你的结论.
 与双曲线
与双曲线 在交点处正交,则椭圆
在交点处正交,则椭圆

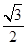

 =1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为
=1(a>b>0)的左焦点为F,右顶点为A,动点M为右准线上一点(异于右准线与x轴的交点),设线段FM交椭圆C于点P,已知椭圆C的离心率为 ,点M的横坐标为
,点M的横坐标为 .
.
 的椭圆
的椭圆 与双曲线
与双曲线 有相同的焦点,且椭圆长轴的端点,短轴的端点,焦点到双曲线的一条渐近线的距离依次构成等差数列,则双曲线
有相同的焦点,且椭圆长轴的端点,短轴的端点,焦点到双曲线的一条渐近线的距离依次构成等差数列,则双曲线 B.
B. C.
C. D.
D.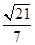
 =1的两焦点为F1、F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为________.
=1的两焦点为F1、F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为________.