Question

在三棱锥P-ABC中，PA，PB，PC两两垂直，PA=PB=PC=1，则P到平面ABC的距离为（　　）

• A．

  3

  3

• B．

  3

• C．1
• D．

  2 3

  3

Answer 1

分析：先确定△ABC是等边三角形，再利用V_A-PBC=V_P-ABC，即可求P到平面ABC的距离．

解答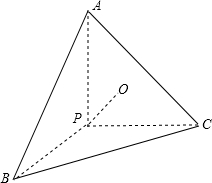：解：设P到平面ABC的距离为h，则
∵三棱锥P-ABC中，PA，PB，PC两两垂直，PA=PB=PC=1，
∴AB=BC=AC=

2

∵V_A-PBC=V_P-ABC
∴

1

3

×

1

2

×1×1×1=

1

3

×

3

4

×(

2

)2h
∴h=

3

3

故选A．

点评：本题考查点到面的距离的计算，考查三棱锥体积的计算，正确运用等体积转化是关键．