题目内容
1．设等差数列{an}的前n项和为Sn，且满足an+Sn=An2+Bn+1（A≠0）则$\frac{B-1}{A}$=3．分析 由于an+Sn=An2+Bn+1（A≠0），可得a1+a1=A+B+1，2a2+a1=4A+2B+1，2a3+a2+a1=9A+3B+1，利用2a2=a1+a2，即可得出．
解答 解：∵an+Sn=An2+Bn+1（A≠0），
∴a1+a1=A+B+1，2a2+a1=4A+2B+1，2a3+a2+a1=9A+3B+1，
解得a1=$\frac{1}{2}（A+B+1）$，a2=$\frac{7}{4}A+\frac{3}{4}B$+$\frac{1}{4}$，a3=$\frac{27}{8}A+\frac{7}{8}B+\frac{1}{8}$，
∵2a2=a1+a2，
∴$\frac{7}{2}A+\frac{3}{2}B+\frac{1}{2}$=$\frac{1}{2}（A+B+1）$+$\frac{27}{8}A+\frac{7}{8}B+\frac{1}{8}$，
化为：3A-B+1=0，
∴$\frac{B-1}{A}$=3．
故答案为：3．
点评 本题考查了递推关系、等差数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
培优三好生系列答案
相关题目
20．定义在R上的偶函数f（x），对任意的实数x都有f（x+4）=-f（x）+2，且f（-3）=3，则f（2015）=（ ）
| A． | -1 | B． | 3 | C． | 2015 | D． | -4028 |
17．若f（x）=$\left\{\begin{array}{l}{{x}^{2}+a，x＜0}\\{{2}^{x}，x≥0}\end{array}\right.$，且f（1）=f（-2），则a=（ ）
| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
4．设a＞0，b＞0，则（ ）
| A． | 若2a+log2a=2b+log3b，则a＜b | B． | 若2a+log2a=2b+log3b，则a＞b | ||
| C． | 若2a+log2a=3b+log2b，则a＜b | D． | 若2a+log2a=3b+log2b，则a＞b |
13．在△ABC中，若条件p：A=60°，条件q：sinA=$\frac{\sqrt{3}}{2}$，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
10．
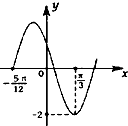已知函数f（x）=Acos（ωx+φ）（x∈R）的图象的一部分如图所示，其中A＞0，ω＞0，|φ|＜$\frac{π}{2}$，为了得到函数f（x）的图象，只要将函数g（x）=2cos2$\frac{x}{2}-2{sin^2}\frac{x}{2}$（x∈R）图象上所有的点（ ）
已知函数f（x）=Acos（ωx+φ）（x∈R）的图象的一部分如图所示，其中A＞0，ω＞0，|φ|＜$\frac{π}{2}$，为了得到函数f（x）的图象，只要将函数g（x）=2cos2$\frac{x}{2}-2{sin^2}\frac{x}{2}$（x∈R）图象上所有的点（ ）| A． | 向右平移$\frac{π}{6}$个单位长度，再把所得各点的横坐标变为原来的$\frac{1}{2}$倍，纵坐标不变 | |
| B． | 向右平移$\frac{π}{6}$个单位长度，再把所得各点的横坐标变为原来的2倍；纵坐标不变 | |
| C． | 向左平移$\frac{π}{3}$个单位长度，再把得所各点的横坐标变为原来的$\frac{1}{2}$倍；纵坐标不变 | |
| D． | 向左平移$\frac{π}{3}$个单位长度，再把所得各点的横坐标变为原来的2倍，纵坐标不变 |
11．将函数y=$\sqrt{3}$sin2x-cos2x的图象向右平移$\frac{π}{4}$个单位长度，所得图象对应的函数为g（x），以下选项正确的是（ ）
| A． | 有最大值，最大值为$\sqrt{3}$+1 | B． | 对称轴方程是x=$\frac{7π}{12}$+kπ，k∈Z | ||
| C． | 在区间[$\frac{π}{12}$，$\frac{7π}{12}$]上单调递增 | D． | 是周期函数，周期T=$\frac{π}{2}$ |